√ — Математические термины; функция. Математические термины все
Математика. Словарь
Абсцисса (латинское слово abscissa - «отрезанная»). Заимствовано из французского языка в начале XIX века Франц. abscisse – из латермин Это одна из декартовых координат точки, обычно первая, обозначаемая буквой x. В современном смысле термин употреблён впервые немецким ученым Готфридом Лейбницем (в 1675 году).
Автоковариация (случайного процесса X(t)). Ковариация X(t) и X(t+h)
Аддитивность (латинское слово additivus – «прибавляемый»). Свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части.
Адъюнкта (латинское слово adjunctus – «присоединенный»). Это то же, что и алгебраическое дополнение.
Аксиома (греческое слово axios- ценный; axioma – «принятие положения», «почет», «уважение», «авторитет»). В рус.яз. – с Петровских времен. Это основное положение, самоочевидный принцип. Впервые термин встречается у Аристотеля. Использовался в книгах Евклида «Начала». Большую роль сыграли работы древнегреческого ученого Архимеда, который сформулировал аксиомы, относящиеся к измерению величин. Вклад в аксиоматику внесли Лобачевский, Паш, Пеано. Логически безупречный список аксиом геометрии был указан немецким математиком Гильбертом на рубеже 19 и 20 вв.
Аксонометрия (от греческие слова akon – «ось» и metrio – «измеряю»). Это один из способов изображения пространственных фигур на плоскости.
Алгебра (араб. слово «ал-джебр». Заимствовано в XVII веке из польск. яз.). Это часть математики, развивающаяся в связи с задачей о решении алгебраических уравнений. Термин впервые появляется у выдающегося среднеазиатского математика и астронома 11 века Мухам меда бен-Мусы ал-Хорезми.
Анализ (греческое слово analozis – «решение», «разрешение»). Термин «аналитическая» восходит к Виету, который отвергал слово «алгебра» как варварское, заменяя его словом «анализ».
Аналогия (греческое слово analogia – «соответствие», «сходство»). Это умозаключение по сходству частных свойств, имеющихся у двух математических понятий.
Антилогарифмлатермин слово nummerus – «число»). Это число, которое имеет данное табличное значение логарифма, обозначается буквой N.
Антье (французское слово entiere – «целый»). Это то же, что целая часть действительного числа.
Апофема (греческое слово apothema,apo – «от», «из»; thema – «приложенное», «поставленное»).
1.В правильном многоугольнике апофема – отрезок перпендикуляра, опущенного из его центра на любую из его сторон, а также его длина.
2.В правильной пирамиде апофема – высота любой его боковой грани.
3.В правильной усеченной пирамиде апофема – высота любой ее боковой грани.
Аппликата (латинское слово applicata – «приложенная»). Это одна из декартовых координат точки в пространстве, обычно третья, обозначаемая буквой Z.
Аппроксимация (латинское слово approximo – «приближаюсь»). Замена одних математических объектов другими, в том или ином смысле близкими к исходным.
Аргумент функции (латинское слово argumentum – «предмет», «знак»). Это независимая переменная величина, по значениям которой определяют значения функции.
Арифметика (греческое слово arithmos – «число»). Это наука, изучающая действия над числами. Арифметика возникла в странах Древнего Востока, Вавилона, Китае, Индии, Египте. Особый вклад внесли: Анаксагор и Зенон, Евклид, Эратосфен, Диофант, Пифагор, Леонардо Пизанский (Фибоначчи) и др.
Арктангенс, Арксинус (приставка «арк»- латинское слово arcus – «лук», «дуга»). Arcsin и arctg появляются в 1772 году в работах венского математика Шеффера и известного французского ученого Ж.Л. Лагранжа, хотя несколько ранее их уже рассматривал Д. Бернулли, но который употреблял другую символику.
Асимметрия (греческое слово asymmetria – «несоразмерность»). Это отсутствие или нарушение симметрии.
Асимптота (греческое слово asymptotes – «несовпадающий»). Это прямая, к которой неограниченно приближаются точки некоторой кривой по мере того, как эти точки удаляются в бесконечность.
Астроида (греческое слово astron – «звезда»). Алгебраическая кривая.
Ассоциативность (латинское слово associatio – «соединение»). Сочетательный закон чисел. Термин введен Уильямом Гамильтоном (в 1843).
Биллион (французское слово billion, или миллиард – milliard). Это тысяча миллионов, число изображаемое единицей с 9 нулями, термине. число 10 9 . В некоторых странах биллионом называют число, равное 10 12.
Бином латермин слова bi – «двойной», nomen – «имя». Это сумма или разность двух чисел или алгебраических выражений, называемых членами бинома.
Биссектриса (латермин слова bis – «дважды» и sectrix –«секущая»). Заимствовано В XIX века из французского языка где bissectrice – восходит к латинское словосочетанию. Это прямая, проходящая через вершину угла и делящая его пополам.
🔝
Вектор (латинское слово vector – «несущий», «носитель»). Это направленный отрезок прямой, у которой один конец называют началом вектора, другой конец – концом вектора. Этот термин ввел ирландский ученый У. Гамильтон (в 1845).
Вертикальные углы (латермин слова verticalis – «вершинный»). Это пары углов с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
🔝
Гексаэдр (греческие слова geks – «шесть» и edra – «грань»). Это шестигранник. Этот термин приписывают древнегреческому ученому Паппу Александрийскому (3 век).
Геометрия (греческие слова geо – «Земля» и metreo – «измеряю»). Др.-рус. Заимствовано из греч.яз. Часть математики, изучающая пространственные отношения и формы. Термин появился в 5 веке до нашей эры в Египте, Вавилоне.
Гипербола (греческое слово hyperballo – «прохожу через что-либо»). Заимствовано в XVII веке из латыни Это незамкнутая кривая из двух неограниченно простирающихся ветвей. Терминввел древнегреческий ученый Апполоний Пермский.
Гипотенуза (греческое слово gyipotenusa – «стягивающая»). Заимствовано из латыни в XVII веке, в котором hypotenusa – от греч. сторона прямоугольного треугольника, лежащая против прямого угла. Древнегреческий ученый Евклид (3 век до нашей эры) вместо этого термина писал, «сторона, которая стягивает прямой угол».
Гипоциклоида (греческое слово gipo – «под», «внизу»). Кривая, которую при этом описывает точка окружности.
Гониометрия (латинское слово gonio – «угол»). Это учение о «тригонометрических» функциях. Однако это название не привилось.
Гомотетия (греческое слово homos- «равный», «одинаковый», thetos - «расположенный»). Это расположение подобных между собой фигур, при котором прямые, соединяющие соответствующие друг другу точки фигур, пересекаются в одной и той же точке, называемой центром гомотетии.
Градус (латинское слово gradus – «шаг», «ступень»). Единица измерения плоского угла, равная 1/90 части прямого угла. Измерение углов в градусах появилось более 3 лет назад в Вавилоне. Обозначения, напоминающие современные, использовались древнегреческими ученым Птолемеем.
График (греческое слово graphikos- «начертанный»). Это график функции – кривая на плоскости, изображаемая зависимость функции от аргумента.
🔝
Дедукция (латинское слово deductio-«выведение»). Это форма мышления, посредством которой утверждение выводится чисто логически (по правилам логики) из некоторых данных утверждений – посылок.
Деференты (латинское слово defero-«несу», «перемещаю»). Это окружность, по которой вращаются эпициклоиды каждой планеты. У Птолемея планеты вращаются по окружностям – эпициклам, а центры эпициклов каждой планеты вращаются вокруг Земли по большим окружностям – деферентам.
Диагональ (греческое слово dia – «через» и gonium – «угол»). Это отрезок прямой, соединяющий две вершины многоугольника, не лежащие на одной стороне. Термин встречается у древнегреческого ученого Евклида (3 век до нашей эры).
Диаметр (греческое слово diametros – «поперечник», «насквозь», «измеряющий» и слово dia – «между», «сквозь»). Термин «деление» в русском языке впервые встречаются у Леонтия Филлиповича Магницкого .
Директриса (латинское слово directrix – «направляющий»).
Дискретность (латинское слово discretus – «разделенный», «прерывистый»). Это прерывность; противопоставляется непрерывности.
Дискриминант (латинское слово discriminans- «различающий», «разделяющий»). Это составленное из величин, определенных заданную функцию, выражение, обращением которого в нуль характеризуется то или иное отклонение функции от нормы.
Дистрибутивность (латинское слово distributivus – «распределительный»). Распределительный закон, связывающий сложение и умножение чисел. Термин ввел франц. ученый Ф. Сервуа (в 1815 году).
Дифференциал (латинское слово differento- «разность»). Это одно из основных понятий математического анализа. Этот термин встречается у немецкого ученого Г. Лейбница в 1675 г. (опубликовано в 1684году).
Дихотомия (греческое слово dichotomia – «разделение надвое»). Способ классификации.
Додекаэдр (греческие слова dodeka – «двенадцать» и edra – «основание»). Это один из пяти правильных многогранников. Термин впервые встречается у древнегреческого ученого Теэтет (4 век до нашей эры).
🔝
Знаменатель - число, показывающее размеры долей единицы, из которых составлена дробь. Впервые встречается у византийского ученого Максима Плануда (конец XIII века).
Изоморфизм (греческие слова isos – «равный» и morfe – «вид», «форма»). Это понятие современной математики, уточняющее широко распространенное понятие аналогии, модели. Термин был введен в середине XVII века.
Икосаэдр (греческие слова eicosi – «двадцать» и edra – основание). Один из пяти правильных многогранников; имеет 20 треугольных граней, 30 ребер и 12 вершин. Термин дан Теэтетом, который и открыл его (4 век до нашей эры).
Инвариантность (латермин слова in - «отрицание» и varians - «изменяющийся»). Это неизменность какой-либо величины по отношению к преобразованиям координатермин термин введен английским Дж. Сильвестром (в 1851).
Индукция (латинское слово inductio – «наведение»). Один из методов доказательства математических утверждений. Этот метод впервые появляется у Паскаля.
Индекс (латинское слово index – «указатель». Заимствовано в начале XVIII в. из латыни). Числовой или буквенный указатель, которым снабжаются математические выражения для того, чтобы отличать их друг от друга.
Интеграл (латинское слово integro – «восстанавливать» или integer – «целый»). Заимствовано во второй половине XVIII в. из французского языка на базе латермин integralis – «целый», «полный». Одно из основных понятий математического анализа, возникшее в связи потребностью измерять площади, объемы, отыскивать функции по их производным. Обычно эти концепции интеграла связывают с Ньютоном и Лейбницем. Впервые это слово употребил в печати швейцарский Ученый Якоб Бернулли (в 1690 году). Знак ∫ - стилизованная буква S от латермин слова summa – «сумма». Впервые появился у Готфрида Вильгельма Лейбница.
Интервал (латинское слово intervallum – «промежуток», «расстояние»). Множество действительных чисел, удовлетворяющее неравенству a < x <b.
Иррациональное число (термин слово irrationalis – «неразумный»). Число, не являющееся рациональным. Термин ввел немецк. ученый Михаэль Штифель (в 1544 году). Строгая теория иррациональных чисел была построена во 2-ой половине XIX века.
Итерация (атермин слово iteratio – «повторение»). Результат повторного применения какой-либо математической операции.
🔝
Калькулятор - немецкое слово kalkulator восходит к латермин слову calculator – «считать». Заимствовано в конце XVIII в. из немец. яз. Портативное вычислительное устройство.
Каноническое разложение - греческое слово canon – «правило», «норма».
Касательная - латинское слово tangens – «касающийся». Семантическая калька конца 18 века.
Катет - латинское слово katetos – «отвес». Сторона прямоугольного треугольника, прилежащая к прямому углу. Термин впервые встречается в форме «катетус» в «Арифметике» Магницкого 1703 года, но уже во втором десятилетии 18 века получает распространение современная форма.
Квадрат - латинское слово quadratus – «четырехугольный» (от guattuor - «четыре»). Прямоугольник, у которого все стороны равны, или, что равносильно, ромб, у которого все углы равны.
Кватернионы - латинское слово quaterni – «по четыре». Система чисел, возникшая при попытках найти обобщение комплексных чисел. Термин предложен английским Гамильтоном (в 1843 году).
Квинтиллион - французское quintillion. Число, изображаемое единицей с 18 нулями. Заимствовано в конце XIX века.
Ковариация (корреляционный момент, ковариационный момент) — в теории вероятностей и математической статистике мера линейной зависимости двух случайных величин. wikipedia. ENG: Covariance
Коллинеарность - латинское слово con, com – «вместе» и linea - «линия». Расположенность на одной линии (прямой). Термин ввел америк. ученый Дж.Гиббс; впрочем, это понятие встречалось ранее у У. Гамильтона (в 1843).
Комбинаторика - латинское слово combinare – «соединять». Раздел математики, в котором изучаются различные соединения и размещения, связанные с подсчетом комбинаций из элементов данного конечного множества.
Компланарность - латерминслова con, com – «вместе» и planum – «плоскость». Расположение в одной плоскости. Термин впервые встречается у Я.Бернулли; впрочем, это понятие встречалось ранее у У.Гамильтона (в 1843).
Коммутативность - позднелатинское слово commutativus – «меняющийся». Свойство сложения и умножения чисел, выражаемое тождествами: a+b=b+a , ab=ba.
Конгруэнтность - латинское слово congruens – «соразмерный». Термин, употребляемый для обозначения равенства отрезков, углов, треугольников и др.
Константа - латинское слово constans–«постоянный», «неизменный». Постоянная величина при рассмотрении математических и др. процессов.
Конус - греческое слово konos – «кегля», «шишка», «верхушка шлема». Тело, ограниченное одной полостью конической поверхности и пересекающей эту полость плоскостью, перпендикулярной ее оси. Термин получил современный смысл у Аристарха, Евклида, Архимеда.
Конфигурация - латинское слово со – «вместе» и figura - «вид». Расположение фигур.
Конхоида - греческое слово conchoides – «подобная раковине мидии». Алгебраическая кривая. Ввел Никомед из Александрии (2 век до нашей эры).
Координаты - латинское слово со – «вместе» и ordinates - «определенный». Числа, взятые в определенном порядке, определяющие положение точки на линии, плоскости, пространстве. Термин ввел Г. Лейбниц (в 1692).
Косеканс - латинское слово cosecans. Одна из тригонометрических функций.
Косинус - латинское слово complementi sinus, complementus – «дополнение», sinus – «впадина». Заимствовано в конце XVIII в. из языка ученой латыни. Одна из тригонометрических функций, обозначаемая cos. Ввел Леонард Эйлер в 1748 году.
Котангенс - латинское слово complementi tangens: complementus – «дополнение» или от латермин слова cotangere – «соприкасаться». Во второй половине XVIII в. из языка научной латыни. Одна из тригонометрических функций, обозначается ctg.
Коэффициент - латинское слово со – «вместе» и efficiens – «производящий». Множитель, обычно выражаемый цифрами. Термин ввел Виетермин
Куб - греческое слово kubos – «игральная кость». Заимствовано в конце XVIII в. из ученой латыни. Один из правильных многогранников; имеет 6 квадратных граней, 12 ребер, 8 вершин. Название введено пифагорейцами, затем встречается у Евклида (3 век до нашей эры).
🔝
Лемма - греческое слово lemma – «допущение». Это вспомогательное предложение, употребляемое при доказательствах других утверждений. Термин введен древнегреческими геометрами; особенно часто встречается у Архимеда.
Лемниската - греческое слово lemniscatus – «украшенный лентами». Алгебраическая кривая. Изобрел Бернулли.
Линия - латинское слово linea – «лен», «нить»,«шнур», «веревка». Один из основных геометрических образов. Представлением о ней может служить нить или образ, описываемый движением точки в плоскости или пространстве.
Логарифм - греческое слово logos – «отношение» и arithmos – «число». Заимствовано в XVII веке из французского языка, где logarithme - англ. logarithmus – образовано сложением греч. слов. Показатель степени m, в которую необходимо возвести a, чтобы получить N.термин предложил Дж. Непер.
🔝
Максимум - латинское слово maximum – «наибольшее». Заимствовано во второй половине XIX века из латыни Наибольшее значение функции на множестве определения функции.
Мантисса - латинское слово mantissa – «прибавка». Это дробная часть десятичного логарифма. Термин был предложен российским математиком Леонардом Эйлер (в 1748).
Масштаб - немецк. слово mas – «мера» и stab – палка». Это отношение длины линии на чертеже к длине соответствующей линии в натуре.
Математика - греческое слово matematike от греческие слова matema – «знание», «наука». Заимствовано в начале XVIII в. из латыни, где mathematica – греческая Наука о количественных отношениях и пространственных формах действительного мира.
Матрица - латинское слово matrix – «матка», «источник», «начало». Это прямоугольная таблица, образованная из некоторого множества и состоящая из строк и столбцов. Впервые термин появился у Уильяма Гамильтона и ученых А. Кэли и Дж. Сильвестра в сер. XIX века. Современное обозначение – две вертик. черточки - ввел А. Кэли (в 1841).
Медиана (треуг-ка) - латинское слово medianus – «средний». Это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Метр - французское слово metre – «палка для измерения» или греческое слово metron – «мера». Заимствовано в XVII веке из французского языка, где metre – греч. Это основная единица длины. Она появилась на свет 2 века назад. Метр был «рожден» Великой французской революцией в 1791 году.
Метрика - греческое слово metrike < metron – «мера», «размер». Это правило определения расстояния между любыми двумя точками данного пространства.
Миллион - итальянское слово millione – «тысячище». Заимствовано в Петровскую эпоху из французского языка, где million – итальянское Число, записанное с шестью нулями. Термин придумал Марко Поло.
Миллиард - французское слово mille – «тысяча». Заимствовано в XIX века из французского языка, где milliard – суф. Производное от mille – «тысяча».
Минимум - латинское слово minimum – «наименьшее». Наименьшее значение функции на множестве определения функции.
Минус - латинское слово minus – «менее». Это математический знак в виде горизонтальной черты, употребляемый для обозначения отрицательных чисел и действия вычитания. Введен в науку Видманом в 1489 году.
Минута - латинское слово minutus – «мелкий», «уменьшенный». Заимствовано в начале XVIII в. из французского языка, где minute – латермин Это единица измерения плоских углов, равная 1/60 градуса.
Модуль - латинское слово modulus – «мера», «величина». Это абсолютная величина действительного числа. Термин ввел Роджер Котс , ученик Исаака Ньютона. Знак модуля введен в 19 веке Карлом Вейерштрассом.
Мультипликативность - латинское слово multiplicatio – «умножение». Это свойство функции Эйлера.
🔝
Норма - латинское слово norma – «правило», «образец». Обобщение понятия абсолютной величины числа. Знак «нормы» ввел немецкий учёный Эрхард Шмидт (в 1908 году).
Нуль - латинское слово nullum–«ничто», «никакой». Первоначально термин обозначал отсутствие числа. Обозначение нуля появилось около середины первого тысячелетия до нашей эры
Нумерация - латинское слово numero – «считаю». Это счисление или совокупность приемов наименования и обозначения чисел.
🔝
Овал - латинское слово ovaum – «яйцо».Заимствовано в XVII веке из франц., где ovale – латермин Это замкнутая выпуклая плоская фигура.
Окружность греческое слово periferia – «периферия», «окружность». Это множество точек плоскости, находящихся на данном расстоянии от данной точки, лежащей в той же плоскости и называемой ее центром.
Октаэдр - греческие слова okto – «восемь» и edra – «основание». Это один из пяти правильных многогранников; имеет 8 треугольных граней, 12 ребер и 6 вершин. Этот термин дан древнегреческим ученым Теэтетом (4 век до н.э), который впервые и построил октаэдр.
Ордината - латинское слово ordinatum – «по порядку». Одна из декартовых координат точки, обычно вторая, обозначаемая буквой y. Как одна из декартовых координат точки, этот термин употреблён немецким ученым Готфридом Лейбницем (в 1694 году).
Орт - греческое слово ortos – «прямой». То же, что единичный вектор, длина которого принята равной единице. Термин ввел английский ученый Оливер Хевисайд (в 1892 году).
Ортогональность - греческое слово ortogonios – «прямоугольный». Обобщение понятие перпендикулярности. Встречается у древнегреческого ученого Евклида (3 век до нашей эры).
🔝
Парабола - греческое слово parabole – «приложение».Это нецентральная линия второго порядка, состоящая из одной бесконечной ветви, симметричной относительно оси. Термин ввел древнегреческий ученый Аполлоний Пергский, рассматривавший параболу как одно из конических сечений.
Параллелепипед - греческое слово parallelos- «параллельный» и epipedos – «поверхность». Это шестигранник, все грани которого – параллелограммы. Термин встречался у древнегреческих ученых Евклида и Герона.
Параллелограмм - греческие слова parallelos – «параллельный» и gramma – «линия», «черта». Это четырехугольник, у которого противоположные стороны попарно параллельны. Термин начал употреблять Евклид.
Параллельность - parallelos – «рядом идущий». До Евклида термин употреблялся в школе Пифагора.
Параметр - греческое слово parametros – «отмеривающий». Это вспомогательная переменная, входящая в формулы и выражения.
Периметр - греческое слово peri – «вокруг», «около» и metreo – «измеряю». Термин встречается у древнегреческих ученых Архимеда (3 век до нашей эры), Герона (в 1 веке до нашей эры), Паппа (3 век).
Перпендикуляр - латинское слово perpendicularis – «отвесный». Это прямая, пересекающая данную прямую (плоскость) под прямым углом. Термин был образован в средние века.
Пирамида - греческое слово pyramis, котермин произошло от егип.слова permeous – «боковое ребро сооружения» или от pyros –«пшеница», или от pyra – «огонь». Заимствовано из стермин-сл. яз. Это многогранник, одна из граней которого – плоский многоугольник, а остальные грани – треугольники с общей вершиной, не лежащей в плоскости основания.
Площадь - греческое слово plateia – «широкая». Происхождение неясно. Некоторые ученые считают Заимствовано из стермин-сл. Другие толкуют как исконно русское.
Планиметрия - латинское слово planum – «плоскость» и metreo – «измеряю». Это часть элементарной геометрии, в которой изучаются свойства фигур, лежащих в плоскости. Термин встречается у древнегреч. ученого Евклида (4 век до нашей эры).
Плюс - латинское слово plus – «больше». Это знак для обозначения действия сложения, а также для обозначения положительности чисел. Знак ввел чешский (немецкий) ученый Ян (Иоганн) Видман (в 1489 году).
Полином - греческое слово polis – «многочисленный», «обширный» и латинское слово nomen – «имя». Это то же, что многочлен, термине. сумма некоторого числа одночленов.
Потенцирование - немецкое слово potenzieren – «возводить в степень». Действие, заключающееся в нахождении числа по данному логарифму.
Предел - латинское слово limes – «граница». Это одно из основных понятий математики, означающее, что некоторая переменная величина в рассматриваемом процессе ее изменения неограниченно приближается к определенному постоянному значению. Термин ввел Ньютон, а употребляемый ныне символ lim (3 первые буквы от limes) – французский учёный Симон Люилье (в 1786 году). Выражение lim первым записал ирландский математик Уильям Гамильтон (в 1853 году).
Призма - греческое слово prisma – «отпиленный кусок». Это многогранник, две грани которого – равные n-угольники, называемые основаниями призмы, а остальные грани – боковые. Термин встречается уже в 3 веке до нашей эры у древнегреч. ученых Евклида и Архимеда.
Пример - греческое слово primus – «первый». Задача с числами. Термин изобрели греческие математики.
Производная - французское derivee. Ввел Жозеф Лагранж в 1797 году.
Проекция - латинское слово projectio – «бросание вперед». Это способ изображения плоской или пространственной фигуры.
Пропорция - латинское слово proportio – «соотношение». Это равенство между двумя отношениями четырех величин.
Процент - латинское слово pro centum - «со ста». Идея процента возникла в Вавилоне.
Постулат - латинское слово postulatum – «требование». Употребляемое иногда название для аксиом математической теории
🔝
Радиан - латинское слово radius – «спица», «луч». Это единица измерения углов. Первое издание, содержащее этот термин, появилось в 1873 году в Англии.
Радикал - латинское слово radix – «корень», radicalis – «коренной». Современный знак √ впервые появился в книге Рене Декарта «Геометрия», изданной в 1637 году. Этот знак состоит из двух частей: модифицированной буквы r и черты, заменявшей ранее скобки. Индийцы называли «мула», арабы – «джизр», европейцы – «радикс».
Радиус - латинское слово radius – «спица в колесе». Заимствовано в Петровскую эпоху из латыни Это отрезок, соединяющий центр окружности с какой-либо ее точкой, а также длина этого отрезка. В древности термин не было, он встречается впервые в 1569 г. у французского ученого Пьра Раме, затем у Француа Виета и становится общепринятым в конце XVII века.
Рекуррентный - латинское слово recurrere – «возвращаться назад». Это возвратное движение в математике.
Ромб - греческое слово rombos – «бубен». Это четырехугольник, у которого все стороны равны. Термин употребляется у древнегреческих ученых Герона (в 1 век до нашей эры), Паппа (2-ая половина 3 века).
Рулетты - французское roulette – «колесико», «сравните», «рулетка», «руль». Это кривые. Термин придумали франц. математики, изучавшие свойство кривых.
🔝
Сегмент - латинское слово segmentum – «отрезок», «полоса». Это часть круга, ограниченная дугой граничной окружности и хордой, соединяющей концы этой дуги.
Секанс - латинское слово secans – «секущая». Это одна из тригонометрических функций. Обозначается sec.
Секстиллион - французское sextillion. Число, изображаемое с 21 нулем, термине. число 1021.
Сектор - латинское слово seco – «режу». Это часть круга, ограниченная дугой его граничной окружности и двумя ее радиусами, соединяющими концы дуги с центром круга.
Секунда - латинское слово secunda – «вторая». Это единица измерения плоских углов, равная 1/3600 градуса или 1/60 минуты.
Сигнум - латинское слово signum – «знак». Это функция действительного аргумента.
Симметрия - греческое слово simmetria – «соразмерность». Свойство формы или расположения фигур симметрично.
Синус - латермин sinus –«изгиб», «кривизна», «пазуха». Это одна из тригонометрических функций. В 4-5 вв. называли «ардхаджива» (ардха – половина, джива – тетива лука). Арабскими математиками в 9 в. слово «джайб» - выпуклость. При переводе арабских математических текстов в 12 в. Термин был заменен «синусом». Современное обозначение sin ввел российский ученый Эйлер (в 1748 году).
Скаляр - латинское слово scalaris – «ступенчатый». Это величина, каждое значение которой выражается одним числом. Этот термин ввел ирландский ученый У.Гамильтон (в 1843 году).
Спираль - греческое слово speria – «виток». Это плоская кривая, которая обычно обходит вокруг одной (или нескольких) точки, приближаясь или удаляясь от нее.
Стереометрия - греческие слова stereos – «объемный» и metreo – «измеряю». Это часть элементарной геометрии, в которой изучаются пространственные фигуры.
Сумма - латинское слово summa – «итог», «общее количество». Результат сложения. Знак ? (греч. буква «сигма») ввел российский ученый Леонард Эйлер (в 1755 году).
Сфера - греческое слово sfaira – «шар», «мяч». Это замкнутая поверхность, получаемая вращением полуокружности вокруг прямой, содержащей стягивающий ее диаметр. Терминвстречается у древнегреческих ученых Платона, Аристотеля.
🔝
Тангенс - латинское слово tanger – «касаться». Одна из тригонометр. функций. Термин введен в 10 веке арабским математиком Абу-л-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Обозначение tg ввел российский ученый Леонард Эйлер.
Теорема - греческое слово tereo – «исследую». Это математическое утверждение, истинность которого установлена путем доказательства. Термин употребляется еще Архимедом.
Тетраэдр - греческие слова tetra – «четыре» и edra – «основание». Один из пяти правильных многранников; имеет 4 треугольные грани, 6 ребер и 4 вершины. По-видимому, термин впервые употреблен древнегреческим ученым Евклидом (3 век до нашей эры).
Топология - греческое слово topos – «место». Ветвь геометрии, изучающая свойства геометрических фигур, связанных с их взаимным расположением. Так считали Эйлер, Гаусс, Риман, что термин Лейбница относится именно к этой ветви геометрии. Во второй половине прошлого столетия в новую область математики, она получила название топологии.
Точка - русс. слово «ткнуть» как бы результат мгновенного прикосновения, укола. Н.И.Лобачевский, впрочем, считал, что термин происходит от глагола «точить» - как результат прикосновения острия отточенного пера. Одно из основных понятий геометрии.
Трактриса - латинское слово tractus – «вытянутый». Плоская трансцендентная кривая.
Транспозиция - латинское слово transpositio – «перестановка». В комбинаторике перестановка элементов данной совокупности, при которой меняются местами 2 элемента.
Транспортир - латинское слово transortare – «переносить», «перекладывать». Приспособление для построения и измерения углов на чертеже.
Трансцендентный - латинское слово transcendens –«выходящий за пределы», «переходящий». Его впервые употребил немецкий учёный Готфрид Лейбниц (в 1686 г).
Трапеция - греческое слово trapezion – «столик». Заимствовано в XVII веке из латыни, где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Термин встречается впервые у древнегреческого ученого Посидония (2 век до нашей эры).
Триангулированная - латинское слово triangulum – «треугольник».
Тригонометрия - греческие слова trigonon – «треугольник» и metreo –«измеряю». Заимствовано в XVII веке из ученой латыни. Раздел геометрии, в котором изучаются тригонометрические функции и их приложения к геометрии. Термин впервые встречается в заглавии книги немецкого ученого Б.Титиска (в 1595 году).
Триллион - французское слово trillion. Заимствовано в XVII веке из французского языка Число с 12 нулями, термине. 1012.
Трисекция - угла латерминслова tri – «три» и section – «разрезание», «рассечение». Задача о разделении угла на три равные части.
Трохоида - греческое слово trochoeides – «колесообразный», «круглый». Плоская трансцендентная кривая.
🔝
Угол - латинское слово angulus – «угол». Геометрическая фигура, состоящая из двух лучей с общим началом.
Уникурсальный - латермин слова unus – «один», cursus – «путь». Маршрут обхода всех ребер построенного графа, при котором ни одно ребро не проходит дважды.
🔝
Факториал (k) - латинское слово factor – «множитель». Впервые появился у французского математика Луи Арбогаста. Обозначение k ввел немецкий математик Кретьен Крамп.
Фигура - латинское слово figura – «внешний вид», «образ». Термин применяемый к разнообразным множествам точек.
Фокус - латинское слово focus – «огонь», «очаг». Расстояние до данной точки. Арабы называли параболу «зажигательным зеркалом», а точку, в которой собираются солнечные лучи – «местом зажигания». Кеплер в «Оптической астрономии» перевел этот термин словом «фокус».
Формула - латинское слово formula – «форма», «правило». Это комбинация математических знаков, выражающая какое-либо предложение.
Функция - латинское слово functio – «исполнение», «совершение». Одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Термин впервые появляется в 1692 г. у немецкого ученого Готфрид Лейбница притом не в современном понимании. Термин, близкий к современному встречается у швейцарского ученого Иогана Бернулли (в 1718 году). Обозначение функции f(x) ввел российский ученый Леонард Эйлер (в 1734 году).
🔝
Характеристика - греческое слово character – «признак», «особенность». Целая часть десятичного логарифма. Термин был предложен английским ученым Генри Бригсом (в 1624 году).
Хорда - греческое слово horde – «струна», «тетива». Отрезок, соединяющий две точки окружности.
🔝
Центр - латинское слово centrum – «острие ножки циркуля», «колющее орудие». Заимствовано в XVII веке из латермин Середина чего-либо, например круга.
Циклоида - греческое слово kykloeides – «кругообразный». Кривая, которую описывает отмеченная точка окружности, катящяяся без скольжения по прямой.
Цилиндр - греческое слово kilindros – «валик», «каток». Заимствовано в XVII веке из нем. яз., где zilinder – латермин, но восходящее к греч. kylindros. Это тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, перпендикулярными ее оси. Термин встречается у древнегреческих ученых Аристарха, Евклида.
Циркуль - латинское слово circulus – «круг», «обод». Заимствовано в первой трети XIX века из латыни Прибор для вычерчивания дуг, окружностей, линейных измерений.
Циссоида - греческое слово kissoeides – «плющевидный». Алгебраическая кривая. Изобрел греческий математик Диоглес (2 век до нашей эры).
Цифры - латерминслова cifra – «цифра», происходящего от арабск.слова «сифр», означающего «нуль».
🔝
Числитель - число, показывающее из скольких частей составлена дробь. Термин впервые встречается у византийского ученого Максима Плануда (конец XIII века).
Число Π - (от начальной буквы греческого слова perimetron – «окружность», «периферия»). Отношение длины окружности к ее диаметру. Впервые появилось у валлийского математика Уильяма Джонса (в 1706 году). Стало общепринятым после 1736 года. Π = 3,141592653589793238462…
🔝
Шкала - латинское слово scalae – «ступень». Последовательность чисел, служащая для количественной оценки каких-либо величин.
Эвольвента - латинское слово evolvens – «разворачивающий». Развертка кривой.
Экспонента - латинское слово exponentis – «показывающий». То же, что и экспоненциальная функция. Термин ввел немецкий ученый Готфрид Лейбниц (1679, 1692).
Экстраполирование - латерминслова extra – «сверх» и polio – «приглаживаю», «выправляю». Продолжение функции за пределы ее области определения, при котором продолженная функция принадлежит заданному классу.
Экстремум - латинское слово exstremum – «крайнее». Это общее название максимума и минимума функции.
Эксцентриситет - латерминслова ex – «из», «от» и centrum – «центр». Число, равное отношению расстояния от точки конического сечения до фокуса к расстоянию от этой точки до соответственной директрисы.
Эллипс - греческие слова ellipsis – «недостаток». Это овальная кривая. Термин ввел древнегреческий ученый Апполоний Пергский (260-190 года до нашей эры).
Энтропия - греческое слово entropia- «поворот», «превращение».
Эпициклоида - греческие слова epi – «над», «на» и kykloeides – «кругообразный». Это плоская кривая, описываемая точкой окружности.
А Б В Г Д З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э
Источник - mat-analiz.ru
Другие словари:
Словарь по физике
Аббревиатуры ядерной энергетики
Термины RFID индустрии - на английском языке
| Рекомендую наш хостинг beget.ru |
| Пишите на www.andreyolegovich.ru cобака yandex.ru если Вы: |
| 1. Хотите написать статью для моего сайта или перевести статью на свой родной язык. |
| 2. Хотите разместить на сайте рекламу, подходящуюю по тематике. |
| 3. Реклама на моём сайте имеет максимальный уровень цензуры. Если Вы увидели рекламный блок недопустимый для просмотра детьми школьного возраста, вызывающий шок или вводящий в заблуждение - пожалуйста свяжитесь со мной по электронной почте |
| 4. Нашли на сайте ошибку, неточности, баг и т.д. ... ....... |
| 5. Статьи можно расшарить в соцсетях, нажав на иконку сети: |
www.andreyolegovich.ru
Словарь математических терминов (буквы А — Д)
Матема́тика (др.-греч. μᾰθημᾰτικά < др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке. Математика не относится к естественным наукам, но широко используется в них как для точной формулировки их содержания, так и для получения новых результатов. Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы.
Представляем вашему вниманию словарь математических терминов.
Абсцисса — (лат. слово abscissa — «отрезанная»). Заимств. из франц. яз. в начале 19 в. Франц. abscisse – из лат. Это одна из декартовых координат точки, обычно первая, обозначаемая буквой x. В современном смысле Т. употреблен впервые немецким ученым Г. Лейбницем (1675).
Аддитивность — (лат. слово additivus – «прибавляемый»). Свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части.
Адъюнкта — (лат. слово adjunctus – «присоединенный»). Это то же, что и алгебраическое дополнение.
Аксиома — (греч. слово axios- ценный; axioma – «принятие положения», «почет», «уважение», «авторитет»). В рус.яз. – с Петровских времен. Это основное положение, самоочевидный принцип. Впервые Т. встречается у Аристотеля. Использовался в книгах Евклида «Начала». Большую роль сыграли работы древнегреческого ученого Архимеда, который сформулировал аксиомы, относящиеся к измерению величин. Вклад в аксиоматику внесли Лобачевский, Паш, Пеано. Логически безупречный список аксиом геометрии был указан немецким математиком Гильбертом на рубеже 19 и 20 вв.
Аксонометрия — (от греч. слова akon – «ось» и metrio – «измеряю»). Это один из способов изображения пространственных фигур на плоскости.
Алгебра — (араб. слово «ал-джебр»). Это часть математики, развивающаяся в связи с задачей о решении алгебраических уравнений. Т. впервые появляется у выдающегося математика и астронома 11 века Мухаммеда бен-Мусы ал-Хорезми.
Анализ — (греч. слово analozis – «решение», «разрешение»). Т. «аналитическая» восходит к Виету, который отвергал слово «алгебра» как варварское, заменяя его словом «анализ».
Аналогия — (греч. слово analogia – «соответствие», «сходство»). Это умозаключение по сходству частных свойств, имеющихся у двух математических понятий.
Антилогарифм — (лат. слово nummerus – «число»). Это число, которое имеет данное табличное значение логарифма, обозначается буквой N.
Антье — (франц. слово entiere – «целый»). Это то же, что целая часть действительного числа.
Апофема — (греч. слово apothema,apo – «от», «из»; thema – «приложенное», «поставленное»).1.В правильном многоугольнике апофема – отрезок перпендикуляра, опущенного из его центра на любую из его сторон, а также его длина.2.В правильной пирамиде апофема – высота любой его боковой грани.3.В правильной усеченной пирамиде апофема – высота любой ее боковой грани.
Аппликата — (лат. слово applicata – «приложенная»). Это одна из декартовых координат точки в пространстве, обычно третья, обозначаемая буквой Z.
Аппроксимация — (лат.слово approximo – «приближаюсь»). Замена одних математических объектов другими, в том или ином смысле близкими к исходным.
Аргумент функции (лат. слово argumentum – «предмет», «знак»). Это независимая переменная величина, по значениям которой определяют значения функции.
Арифметика (греч. слово arithmos – «число»). Это наука, изучающая действия над числами. Арифметика возникла в странах Др. Востока, Вавилона, Китае, Индии, Египте. Особый вклад внесли: Анаксагор и Зенон, Евклид, Эратосфен, Диофант, Пифагор, Л. Пизанский и др.
Арктангенс, Арксинус (приставка «арк»- лат. слово arcus – «лук», «дуга»). Arcsin и arctg появляются в 1772 году в работах венского математика Шеффера и известного французского ученого Ж.Л. Лагранжа, хотя несколько ранее их уже рассматривал Д. Бернулли, но который употреблял другую символику.
Асимметрия (греч. слово asymmetria – «несоразмерность»). Это отсутствие или нарушение симметрии.
Асимптота (греч. слово asymptotes – «несовпадающий»). Это прямая, к которой неограниченно приближаются точки некоторой кривой по мере того, как эти точки удаляются в бесконечность.
Астроида (греч. слово astron – «звезда»). Алгебраическая кривая.
Ассоциативность (лат. слово associatio – «соединение»). Сочетательный закон чисел. Т. введен У.Гамильтоном (1843).
Биллион (франц. слово billion, или миллиард – milliard). Это тысяча миллионов, число изображаемое единицей с 9 нулями, т.е. число 10 9 . В некоторых странах биллионом называют число, равное 10 12.
Бином (лат. слова bi – «двойной», nomen – «имя) сумма или разность двух чисел или алгебраических выражений, называемых членами бинома.
Биссектриса (лат. слова bis – «дважды» и sectrix –«секущая»). Заимств. В 19 в. из франц. яз. где bissectrice – восходит к лат. словосочетанию. Это прямая, проходящая через вершину угла и делящая его пополам.
Вектор (лат. слово vector – «несущий», «носитель»). Это направленный отрезок прямой, у которой один конец называют началом вектора, другой конец – концом вектора. Этот термин ввел ирландский ученый У. Гамильтон (1845).
Вертикальные углы (лат. слова verticalis – «вершинный»). Это пары углов с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
Гексаэдр (греч. слова geks – «шесть» и edra – «грань»). Это шестигранник. Этот Т. приписывают древнегреческому ученому Паппу Александрийскому (3 век).
Геометрия (греч. слова geо – «Земля» и metreo – «измеряю»). Др.-рус. заимств. из греч.яз. Часть математики, изучающая пространственные отношения и формы. Т. появился в 5 веке до н.э. в Египте, Вавилоне.
Гипербола (греч. слово hyperballo – «прохожу через что-либо»). Заимств. в 18 в. из лат. яз. Это незамкнутая кривая из двух неограниченно простирающихся ветвей. Т.ввел древнегреческий ученый Апполоний Пермский.
Гипотенуза (греч.слово gyipotenusa – «стягивающая»). Замств. из лат. яз. в 18 в., в котором hypotenusa – от греч. сторона прямоугольного треугольника, лежащая против прямого угла. Древнегреческий ученый Евклид (3 век до н.э.) вместо этого термина писал, «сторона, которая стягивает прямой угол».
Гипоциклоида (греч. слово gipo – «под», «внизу»). Кривая, которую при этом описывает точка окружности.
Гониометрия (лат. слово gonio – «угол»). Это учение о «тригонометрических» функциях. Однако это название не привилось.
Гомотетия (греч. слово homos- «равный», «одинаковый», thetos — «расположенный»). Это расположение подобных между собой фигур, при котором прямые, соединяющие соответствующие друг другу точки фигур, пересекаются в одной и той же точке, называемой центром гомотетии.
Градус (лат. слово gradus – «шаг», «ступень»). Единица измерения плоского угла, равная 1/90 части прямого угла. Измерение углов в градусах появилось более 3 лет назад в Вавилоне. Обозначения, напоминающие современные, использовались древнегреческими ученым Птолемеем.
График (греч. слово graphikos- «начертанный»). Это график функции – кривая на плоскости, изображаемая зависимость функции от аргумента.
Дедукция (лат. слово deductio-«выведение»). Это форма мышления, посредством которой утверждение выводится чисто логически (по правилам логики) из некоторых данных утверждений – посылок.
Деференты (лат. слово defero-«несу», «перемещаю»). Это окружность, по которой вращаются эпициклоиды каждой планеты. У Птолемея планеты вращаются по окружностям – эпициклам, а центры эпициклов каждой планеты вращаются вокруг Земли по большим окружностям – деферентам.
Диагональ (греч. слово dia – «через» и gonium – «угол»). Это отрезок прямой, соединяющий две вершины многоугольника, не лежащие на одной стороне. Т. встречается у древнегреческого ученого Евклида (3 век до н.э.).
Диаметр (греч. слово diametros – «поперечник», «насквозь», «измеряющий» и слово dia – «между», «сквозь»). Т. «деление» в русском языке впервые встречаются у Л.Ф.Магницкий.
Директриса (лат. слово directrix – «направляющий»).
Дискретность (лат. слово discretus – «разделенный», «прерывистый»). Это прерывность; противопоставляется непрерывности.
Дискриминант (лат. слово discriminans- «различающий», «разделяющий»). Это составленное из величин, определенных заданную функцию, выражение, обращением которого в нуль характеризуется то или иное отклонение функции от нормы.
Дистрибутивность (лат. слово distributivus – «распределительный»). Распределительный закон, связывающий сложение и умножение чисел. Т. ввел франц. ученый Ф. Сервуа (1815 г.).
Дифференциал (лат. слово differento- «разность»). Это одно из основных понятий математического анализа. Этот Т. встречается у немецкого ученого Г. Лейбница в 1675 г. (опубликовано в 1684г.).
Дихотомия (греч.слово dichotomia – «разделение надвое»). Способ классификации.
Додекаэдр (греч. слова dodeka – «двенадцать» и edra – «основание»). Это один из пяти правильных многогранников. Т. впервые встречается у древнегреческого ученого Теэтет (4 век до н.э.).
источник
idum.uz
√ - Математические термины; функция
Математика ( mathematics [ˌmæθ(ə)’mætɪks] ) необходима в той или иной степени для любой науки. Иногда математические знания требуются в исключительно огромных количествах (как, например, в теории струн, в квантовой механике). Иногда достаточно лишь общих представлений в разных областях математики. Чаще всего оказываются востребованными познания в математическом анализе, теории множеств, линейной алгебре, поэтому начинать целесообразно именно с них. Я отлично понимаю, что у многих выработалась сильнейшая аллергия на математику благодаря школе, но нельзя же позволить каким-то глупым людям на всю жизнь лишить тебя удовольствия от изучения и понимания математики… Поэтому я предлагаю преодолеть привычное отторжение и попробовать еще раз.
В математике очень и очень нужны термины ( term [tɜːm] ). Когда мы начинаем что-то исследовать и наталкиваемся на новые явления и закономерности, нам необходимо обозначать их терминами, чтобы мысль могла идти дальше. Это касается не только наук, но и бытовой жизни. Если я хочу попросить тебя включить телевизор, я говорю «включи телек», при этом не отдавая себе отчета в том, что «телек» — это короткий и удобный термин. Представь себе, что было бы, если бы мне пришлось говорить «включи электронное устройство для приёма и отображения изображения и звука, передаваемых по беспроводным каналам или по кабелю»! Впрочем, слово «изображение» тоже является термином, и вообще-то мне тогда следовало бы сказать так: «включи электронное устройство для приёма и отображения объекта, образа, явления, в той или иной степени подобного (но не идентичного) изображаемому, подобие которого достигается либо с помощью использования технологий, опирающихся на те или иные физические законы, либо результатом труда создателя изображения, а также звука, передаваемых по беспроводным каналам или по кабелю». Конечно, каждое слово в этом длинном предложении также является термином…

Никакое познание и даже никакая бытовая жизнедеятельность без терминов невозможна – это ясно. Поэтому в юриспруденции, математике, Селекции восприятий, кулинарии и вообще везде нам жизненно необходимы термины.
Это в общем понятно. Но следует понять и еще кое что. Так как роль терминов в нашей жизни поистине грандиозна, то очень важно ещё и понимать значение этих терминов совершенно точно. Если вместо расчески я возьму утюг, то что получится? Недостаточно точное понимание терминов является огромным препятствием в достижении ясности в любой науке. Возникающая муть отравляет все удовольствие полностью, до основания, так как лишает тебя возможности наслаждаться ясностью.
Обычно в учебниках термины вводятся как бы между делом, создавая впечатление, что они не так уж и важны. И совершенно напрасно. Я уверен, что задаче разъяснения значения того или иного термина необходимо уделять много внимания, чтобы исключить возможность неправильного понимания.
Для начала введем термин «параметр» ( parameter [pə’ræmɪtə] ).

Например, я в горах нашел камень, и задумался — донесу я его до логова, или нет. Необходимо прикинуть – сколько он весит. Я беру его, приподнимаю – кажется, килограмм 12. Отлично, это немного, значит дотащу. Таким образом я примерно прикинул вес камня и сделал из этого полезный вывод.
Но этого еще недостаточно, чтобы я смог понять – точно ли получится у меня его дотащить до логова, ведь камень надо засунуть в рюкзак, надо чтобы он там поместился. Измеряя размеры камня, я понимаю, что в моем рюкзаке для него хватит места. Таким образом, я измерил ширину, длину и высоту камня и сделал из этого еще один полезный вывод.
Вес камня, его длина, ширина и высота – всё это является его признаками – то есть тем, что позволяет мне отличить его от другого камня. Кроме этих признаков существует и бесчисленное количество других. Цвет, форма, запах, вкус, прочность, растворимость, электропроводность, теплопроводность, интенсивность чувства красоты, возникающей тогда, когда я на него смотрю, цена, градиент цвета и прочее и прочее. Некоторые признаки мне в данный момент важны, некоторые – нет.
Вес, длину, стоимость на рынке – всё это и многое другое мы можем с той или иной точностью измерить или оценить. Если у меня есть линейка, то длину камня я смогу измерить с точностью до сантиметра. Если линейки нет, то придется удовлетвориться оценкой «на глаз», что уменьшит точность.
Теперь мы можем дать определение: термином «параметр» мы называем всё, что угодно, что подвергается какому-либо измерению или может быть измерено и выражено в числах, и отражает, таким образом, какое-либо свойство объекта.
Я могу измерить линейкой длину камня? Могу. Могу ли я оценить его длину на глаз? Тоже могу. Значит его длина – измеримая величина. Относится ли «длина» к самому камню? Конечно, ведь мы именно его длину замеряем. Отражает ли, таким образом, эта длина какое-то определенное свойство камня? Конечно. Значит, длина измерима и отражает его свойство, помогает нам отличить его от других камней. Значит, согласно определению, длина – это один из параметров камня.
Чем больше разных параметров какого-либо объекта мы измерим или оценим, тем более точное у меня будет о нём представление.
Яркость света можно измерить? Можно, значит и яркость может быть параметром. Глубину глупости человека тоже можно примерно оценить, поэтому глупость тоже является параметром.
При определении параметра мы использовали слово «измерение» ( measurement [‘meʒəmənt] ). На бытовом уровне нам понятно, что такое «измерить» — это значит оценить что-то, сравнивая его с каким-то эталоном. Даже если мы делаем это в своем воображении. Прикидывая «на глаз» длину камня, я примерно вспоминаю, как выглядит линейка длиной в 30 сантиметров, и в своем воображении я прикладываю эту линейку к камню и делаю свою оценку.
Простейшая форма измерения состоит именно в том, что некоторый объект, обладающий тем же свойством, что и измеряемый (в нашем примере, это свойство – длина), принимается за «единицу измерения» ( unit [‘juːnɪt] ), после чего мы вычисляем – сколько раз эта единица может быть уложена в измеряемом объекте. Например, бамбуковый ствол и моя ладонь тоже обладают свойством «протяженности в пространстве», или «длиной» ( length [leŋθ] ). Принимая длину своей ладони за единицу, я выясняю, что мне требуется 50 раз приложить ладонь к бамбуку, чтобы покрыть его от начала до конца. Отсюда я делаю вывод, что длина бамбука, выраженная в моих ладонях, равняется пятидесяти. Я измерил длину бамбуковой палки в своих ладонях. Моя ладонь стала единицей измерения. Если такие единицы измерения мне неудобны, я могу использовать другие, причем совершенно не обязательно, что это будет именно линейка. Например, я хочу поставить двадцать стульев вдоль стены помещения. Линейки у меня нет, зато есть стена и есть один стул. Этого достаточно! Я беру этот стул и ставлю его с одного края стены, делая карандашом отметку, где я мог бы поставить второй стул. Таким образом, передвигая свой стул, я выясняю, что длина стены примерно равна 21 стулу. Значит 20 стульев точно влезут, даже если я не очень точно проводил свои измерения. В данном случае один стул стал для меня единицей измерения длины стены.
Теперь, когда значение термина «параметр» стала ясна, можно получить удовольствие, читая другие определения, которые еще пять минут назад показались бы совершенно запутанными. Например – из википедии: «параметр — это величина, значения которой служат для различения групп элементов некоторого множества между собой». Мы можем поспорить о том – удачное это определение или нет. Если раньше мы говорили о параметре как о том признаке предмета, который «может быть измерен», то здесь говорится о том, что измерение это производится с определенной целью – чтобы отличить одну группу объектов от других. На самом деле цель совершенно неважна. Конечно, мы можем измерить длину карандашей и сказать, что все те, что короче 10 сантиметров, мы назовем «короткими» (то есть поместим их в условную группу «короткие»), а все те, что от 10 до 15 – средние, и остальные – длинные. Мы можем это сделать, конечно. А можем и не делать, а длина все равно останется параметром карандаша. Поэтому это определение я считаю неудобным, и даже неправильным. Мы можем провести такую оценку определения термина «параметр», потому что хорошо разобрались в том – что это такое вообще – параметр.
До сих пор мы брали объекты – камень, стул, ладонь – то есть что-то такое, длина чего постоянна. Но параметр может быть не только постоянной, но и переменной (или изменяющейся) величиной. Вес камня – величина постоянная, а вот, например, высота живой ёлки – нет. В Гималаях есть сосны с упругим, мягким стволом и с огромными, длиной по 15 сантиметров, мягкими иголками. В треке к Эвересту такие сосны в районе Гокьо довольно невысокие – метра 2-3, в районе Намче они встречаются уже высотой до 10 метров, а на подходе к Лукле уже растут гиганты высотой по 40-50 метров. Я выкопал десяток саженцев и посадил их в мордопоселении вдоль Большой Травяной Полянки, и мне стало интересно – как быстро они будут расти? Я измерил высоту саженца сейчас, и буду измерять её раз в полгода. Разумеется, по мере того, как сосна будет расти, ее параметр «высота» будет меняться, то есть он будет «изменяющейся величиной». То есть изменяющейся величиной называется тот или иной параметр, если его значение изменяется. При этом некоторые параметры могут меняться только в одну сторону – как, например, высота растущей ёлки. Другие параметры могут меняться то в одну, то в другую сторону. Но в любом случае, если параметр не постоянен, то он называется изменяющейся величиной, или, еще короче, «переменной» ( variable [‘vɛərɪəbl] ). Этот термин – «переменная величина» или попросту «переменная» — невероятно часто используется в математике.
В элементарной математике и в жизни мы часто встречаем задачи, в которых одна изменяющаяся величина зависит от другой. Простейшим видом такой закономерности является прямая пропорциональность. Например, прямая пропорциональность имеется между количеством собак и их суммарным количеством ушей. Если А – количество собак, и В — количество ушей, то мы можем написать формулу, отражающую факт прямой пропорциональной зависимости В от А:
В=2А
Число «2» и символ «А» стоят в этой формуле рядом. Это означает, что их необходимо перемножить. Конечно, можно написать так: « 2хА » или так: « 2●А », и нередко так и пишут, но для того, чтобы упростить формулы, мы договоримся, что если между символами не стоит вовсе никакого значка, то это означает, что имеется в виду умножение.
В этой записи нет словосочетания «число собак» — вместо него есть символ ( symbol [‘sɪmbəl] ) «А». И нет словосочетания «число ушей» — есть заменяющий его символ «В». Использование символов удобно, так как запись «число ушей равно числу два, умноженному на число собак» слишком длинная и неудобочитаемая. Использование символов делает подобные записи очень простыми и облегчает те или иные операции, которые мы можем проводить с ними. Термин «формула» ( formula [‘fɔːmjələ] ) и означает любую запись, сделанную в символической форме, и, конечно, имеющую какой-то определенный смысл.
Вместо символов «А» и «В» мы можем выбрать любые другие, разумеется. Исторически сложилось так, что математики чаще всего любят использовать символ «Y» (произносится «игрек») и «X» (произносится «икс»). Если переменных больше чем две, то для третьей чаще всего выбирают символ «Z» ( «зэт» ).
Y=2X
Часто вместо заглавных букв пишут прописные:
y = 2x
Знак « = » читается как «равно» или «равняется», и смысл его интуитивно понятен – он сообщает, что каждому значению икс мы должны подобрать такое значение игрек, чтобы величины в обеих частях уравнения оказались равны.
Почему эту формулу мы считаем именно выражением прямой пропорциональности? Потому что из нее видно, что если количество собак увеличить в 5, или в 10, или во сколько угодно раз, то количество ушей увеличится ровно во столько же раз. У одной собаки два уха, а у десяти собак в десять раз больше ушей, то есть двадцать. Если при увеличении чего-то в несколько раз, количество чего-то другого увеличивается во столько же раз, это и означает, что между ними существует прямая пропорциональность.
Существует ли прямая пропорциональность между игрек и икс в следующей формуле:
y = 2x + 2
Очевидно, что нет. Мы можем проверить это на конкретных примерах. Например, при х=2, у=6, а при х=4, у=10. То есть икс вырос в два раза (с двух до четырех), а игрек вырос с 6 до 10 – не в два раза. Прямой пропорциональности нет.
Теперь немного поработаем над этим уравнением. Обе части уравнения, по определению самого понятия «уравнение», равны. Если от двух равных частей отнять что-то одинаковое, равенство ведь не изменится? Если с обеих чаш уравновешенных весов снять одинаковые гири, равновесие весов не нарушится. Вычтем число 2 из обеих частей, и получим:
у-2 = 2х
Теперь левая часть уравнения прямо пропорциональна правой. Если, например, х = 1, то правая часть уравнения равна 2, а значит и левая часть должна равняться 2, то есть (у-2) должно равняться двум. При удвоенном значении х=2, значение (у-2) также удвоится и будет равняться четырем и т.д. – мы видим прямую пропорциональность. То есть тут (у-2) выступает в роли самостоятельной переменной.
Это может показаться не вполне понятным, поэтому, чтобы легче было это понимать, мы можем ввести в наше уравнение третий символ – «z». Мы можем договориться, что знаком «z» мы будем обозначать величину у, от которой отняли 2. Тогда уравнение будет записано в таком виде, из которого прямая пропорциональность видна теперь уже совершенно ясно:
z = 2x
( при этом z = y-2 )
Пометки типа «при этом»… обычно опускаются, и в результате мы можем записать «систему уравнений», из которых при любом х мы легко вычислим и соответствующее ему у, и наоборот:
z = 2x
z = y-2
Рассмотрим еще один пример. Существует широко известная формула (пока неважно, как она выводится), используя которую мы можем вычислять площадь круга:
S = πR2
Здесь « π » (произносится как «пи») означает некую постоянную величину (постоянную величину часто называют одним словом «константа» ( constant [‘kɔnstənt] )). Она примерно равна 3,14. Символ «S» обозначает площадь круга, а «R» — длину его радиуса (то есть длину отрезка, соединяющего центр круга с любой точкой, лежащей на ограничивающей этот круг окружности).
Запись «R2» является упрощенной записью перемножения R на R. Если нам, к примеру, потребуется четыре раза перемножить R на само себя, то мы не будем писать RRRR, а напишем более просто: R4. Согласись, что так удобней.
В формуле S = πR2 прямой пропорциональности уже нет, и это легко доказать. Предположим, что речь идет о кусте клубники. Клубника изначально заняла круг радиусом R, но через полгода она разрослась так, что радиус этого клубничного круга увеличился в два раза. Поскольку радиус увеличился в два раза, то теперь он стал равняться « 2R ». Подставим это значение в формулу, и переставляя множители так, как нам удобнее (согласно правилам умножения, мы можем переставлять множители), мы получим:
S1 = π(2R)2= π2R2R = π4R2
Сравнивая эту формулу с первой, мы видим, что увеличение радиуса в два раза приводит к увеличению площади круга (то есть к увеличению площади земли, занятой кустом клубники) в четыре раза! (Новую площадь я обозначил как «S1», чтобы не путать с символом «S», обозначающим первоначальную площадь). Такую зависимость мы называем «квадратичной». То есть если некий параметр меняется в три или пять раз, а другой, зависящий от него и только от него параметр, меняется в девять или в двадцать пять раз соответственно, то имеет место «квадратичная зависимость». Можно не говорить каждый раз «в три раза или в пять раз или во сколько-то еще раз», а снова использовать символ. Например, пусть символ «N» будет обозначать любое число, и тогда мы сможем сказать: если некий параметр меняется в N раз, а другой, зависящий от него и только от него параметр, меняется в N2 раз, то имеет место «квадратичная зависимость».
Результаты, вычисленные с помощью этой формулы, можно свести в таблицу:
Глядя на эту таблицу, мы легко замечаем, что площадь растет намного быстрее, чем радиус – радиус вырос с двух до пяти – всего лишь на 3, а площадь – с четырех до двадцати пять, то есть на двадцать один!
Кроме таблиц, существует еще один широко распространенный способ наглядного изображения соотношения между двумя переменными – так называемый «график» ( graphic [‘græfɪk] ). Прежде чем определить — что такое график, введем понятие «осей координат».
Нарисуем горизонтальную линию. На ней отметим любую точку, и обозначим ее как «ноль». Затем отмерим от нуля один сантиметр вправо и обозначим ее как «1» — это означает, что эта точка соответствует числу «1». Еще правее на 1 сантиметр – и мы получаем точку, соответствующую числу «2», и так далее. Математики договорились, что по горизонтали мы будем откладывать числа, соответствующие переменной х. Теперь через точку ноль проведем вертикальную прямую, и отмерим от нуля один сантиметр вверх – эта точка тоже будет соответствовать числу 1, но не для переменной х, а для переменной у. Точка «ноль» называется «началом координат», а сами эти две перпендикулярные друг другу прямые называются «осями координат». Горизонтальную ось часто называют «абсциссой», а вертикальную – «ординатой».
(Можно придумать какое-нибудь дурацкое мнемоническое правило, чтобы запомнить – что есть что. Например, слово «ордината» напоминает «орден» — когда тебе вручают орден, ты стоишь совершенно вертикально, выпрямившись во весь рост, отсюда «ордината» — вертикальная ось).
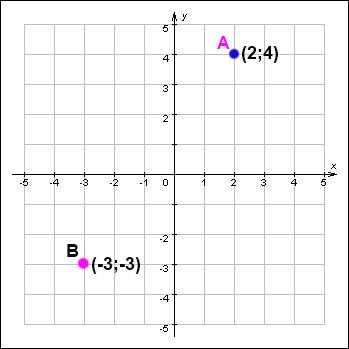
Если нарисовать точку А в произвольном месте на плоскости, на которой заданы оси координат, и через нее провести вертикальную прямую, то место пересечения этой прямой с абсциссой называется «абсциссой этой точки». Иначе говоря, «абсцисса точки графика» — это проекция точки А на ось абсцисс. Аналогично определяется «ордината точки графика». К примеру на нашей картинке абсцисса точки А равна 2, а ордината равна 4. Эта пара чисел называется «координатами» точки. Координаты точки записываются в скобках, при этом абсцисса указывается первой: А(2;4). Легко видеть что полученная пара чисел единственна, так как через заданную точку можно провести только одну единственную прямую, параллельную оси у — двух различных прямых, параллельных оси у, быть не может, значит и точка пересечения этой прямой с осью х может быть только одна.
Так как мы провели две оси координат не под произвольным углом по отношению друг к другу, а именно под прямым, то такие координаты называются «ортогональными» или, иначе, «декартовыми». Чаще всего в математике используются именно ортогональные координаты, так как они облегчают множество операций и очень наглядны. Тем не менее, можно провести ось у под любым другим углом к оси х, например под углом 45 градусов, и это тоже будет система координат, и математики и физики тоже иногда пользуются такими системами, но они уже не являются ортогональными (в будущем мы всегда будем по умолчанию использовать именно ортогональные системы координат).
Если проведенная через точку на плоскости прямая пересекает ось х справа от нуля, то мы ставим ей в соответствие некое положительное число, скажем «+5», а если слева от нуля – то отрицательное число, скажем «-4». Так же обстоит дело и с осью у — все то, что выше нуля, обозначается положительными числами, а что ниже – отрицательными. Поэтому координаты точки В мы запишем так: В(-3;-3).
Любой паре чисел х и у, таким образом, обязательно соответствует какая-нибудь единственная точка на плоскости. Обратное тоже верно – если мы на плоскости поставим какую-нибудь точку, то ей обязательно будет соответствовать единственная пара чисел. Это называется «взаимно-однозначным соответствием».
Можно сказать иначе – между множеством точек на плоскости и множеством пар чисел (x;y) существует взаимно-однозначное соответствие. Такие множества, между которыми существует взаимно-однозначное соответствие, называются «равномощными».
Рассмотрим теперь уравнение:
y = x2
Составим таблицу значений, удовлетворяющих этому равенству:
| х | 1 | 2 | 3 | 4 | 5 |
| у | 1 | 4 | 9 | 16 | 25 |
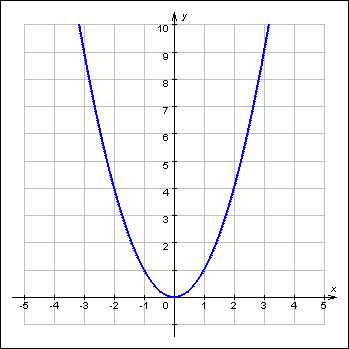
Пользуясь этой таблицей, мы можем нарисовать график (см.справа). По оси х отложим 1, и проведем через эту точку прямую, параллельную оси у. Затем по оси у отложим соответствующее число, то есть тоже 1. Также проведем через эту точку прямую, параллельную оси х. Эти две прямые пересекутся в точке, имеющую координаты (1;1). Таким же образом нарисуем точки с координатами (2;4), затем (3;9) и так далее.
Теперь соединим эти точки плавной (то есть без разрывов и острых углов) кривой линией, или попросту «кривой» ( curve [kɜːv] ), и получим примерный график. Понятно, что если мы хотим, чтобы график был более точным, нам надо будет увеличить количество его точек. Для этого мы должны вычислить значения у для х, равных «1,5», «2.5», «3.5» и так далее, построить новые точки на графике и так далее. Чем больше точек мы возьмем, тем более точным будет график. Но и такая, даже грубо сделанная кривая, позволит нам достаточно точно представлять себе всю совокупность пар (х;у), удовлетворяющих формуле y=x2. Этот метод позволяет легко увидеть некоторые обстоятельства, которые могут быть не так очевидны, если мы перед собой видим только таблицу пар чисел. Например, мы видим, как резко возрастает у при росте х : начерченная кривая круто поднимается вверх, и это показывает, что чем больше х, тем быстрее растет у. Этот метод является, таким образом, чем-то вроде «графической таблицы», при помощи которой мы можем получить примерное значение у для каждого х и наоборот, пользуясь лишь линейкой.
Графический способ имеет то видимое преимущество, что с помощью таблицы, как правило, невозможно определить соответствие полностью – ты же не можешь нарисовать бесконечно огромную таблицу. Если я рассматриваю зависимость длины стержня от его температуры, я конечно могу выписать значения длин для температур 3 или 4 или 5 градусов. Если постараться, я могу даже расширить таблицу и выписать там значения длин для температур 3,5 или 4,5 или 5,5 градусов. Но мыслимо ли выписать еще и длины при температурах 3,455 градуса и т.д.? А вот с помощью графика я могу получить приблизительное значение длины стержня для любой температуры практически мгновенно – всего лишь проведя пару прямых.
Ну и конечно – наглядность взаимозависимости двух величин – огромное преимущество графиков.
Теперь – в конце разъяснения того, что такое график, можно дать его точное определение. Графиком функции (в системе прямоугольных или декартовых координат) называется геометрическое место точек ( locus [‘ləukəs] ), абсциссы ( abscissa [æb’sɪsə] ) которых являются значениями независимой переменной, а ординаты ( ordinate [‘ɔːdɪnət] ) – соответствующими значениями функции. Независимой переменной, то есть той, значение которой мы можем выбрать какую угодно по желанию, в нашем примере является х, а зависимой переменной является y, поскольку если мы задаем какую-то х, то тем самым уже совершенно точно определяем значение y. Если в нашем уравнении х=3, то y может равняться только 9, и ничему другому.
Поэтому математики говорят, что уравнение y=x2 выражает у как функцию от х. Можно сказать иначе: это уравнение задает у как функцию от х. Или так: это уравнение определяет у как функцию от х. Всё равно – можно сказать и так, и так, смысл от этого не меняется, и заключается этот смысл в том, что переменная величина у представлена как математическое выражение, как формула, в которую входит другая переменная величина х, и значение у зависит только от значения х, и не зависит больше ни от каких других переменных.
Коротко говорят об этом так: «игрек – это функция от икс». Услышав такую фразу, мы понимаем, что значение у зависит от того, какое значение принимает х, но совершенно не зависит от того, какие значения будут у каких-то там любых других переменных. Еще мы понимаем, что изменение величины х неизбежно и однозначно влечет за собой изменение величины у.
Если же перед нами уравнение типа:
y =x2 + z
то мы можем сказать, что у — это функция и от х, и от z, то есть это функция от двух переменных.
Мы можем переписать уравнение y = x2 в виде:
х =√у (икс равен квадратному корню из игрек)
и уже теперь мы можем сказать, что икс – функция от игрек, и меняя значения игрек мы будем получать каждый раз соответствующие значения для икс.
Можно сказать и по-другому: «функция – это число, которое ставится в соответствие другому числу в соответствии с заданным правилом». В нашем примере правилом является формула y=x2 , поэтому «функция от двух» будет в нашем случае «четыре» а «функция от десяти» — «сто».
До сих пор я рассматривал только взаимно-однозначные соответствия, но ситуация может быть и другой. Например, у нас в мордологове есть отдельные уровни, на которых растут фруктовые деревья – персики, груши, яблоки, папайя, манго, авокадо, помело, кумкват, мандарины, лимоны, апельсины, гранаты, и куча еще всего разного. Когда мы покупали саженцы, то выбирали такие, у которых стволы раздваивались или растраивались – так кажется красивее. Теперь пронумеруем ямки, в которых растут фруктовые деревья. Затем пронумеруем стволы. Получится, что первый, второй и третий ствол принадлежат дереву, растущему из первой ямки. Четвертый и пятый – из второй, в третьей ямке растет дерево с неразветвленным стволом номер 6 и так далее. Обозначим как у номер ямки, а как x — номер ствола, тогда у нас получится такое соотношение:
| ствол (х) | 1,2,3 | 4,5 | 6 |
| ямка (y) | 1 | 2 | 3 |
Отсюда видно, что каждому стволу соответствует одна и только одна ямка, в то время как каждой ямке могут соответствовать или один, или несколько стволов. В этом примере x также является функцией от у, так как каждому значению у соответствует одно или несколько определенных значений x. Но эта функция уже не взаимно-однозначная, как в предыдущих примерах! Она была бы взаимно-однозначной только в том случае, если бы каждому значению x соответствовало бы только одно значение у, и наоборот — каждому значению у соответствовало бы только одно значение x.
Теперь дадим более широкое определение функции: одна величина называется функцией другой величины, если каждому значению второй величины соответствует одно или несколько определенных значений первой величины. Каким образом задано это соответствие – дело десятое. Это может быть какая-то формула или совершенно произвольное решение, или соответствие может задаваться какими-то внешними причинами типа рассмотренного примера со стволами и ямками и т.д. Важно одно – есть такое соответствие или его нет. Если оно есть – значит у нас есть функция.
Например, график дежурства по кухне мы можем создать совершенно произвольно: в понедельник это один человек, во вторник – другой. Но поскольку теперь каждому дню недели соответствует один человек (или два-три, как они договорятся), то мы можем говорить о том, что нами задана функция, где каждому дню недели соответствует один или несколько человек.
Иногда слово «функция» заменяется словом «зависимая переменная». В примере с площадью круга, величина площади круга является зависимой переменной, а радиус – независимой, если мы сначала рисуем круг определенного радиуса, а затем высчитывает его площадь. Я могу выбрать радиус, какой мне захочется – он является независимой переменной, и этот выбор железобетонно определит величину зависимую – площадь круга.
Определим более точно термин «формула». Формула (или еще иначе говорят «аналитическое выражение») – это совокупность известных математических операций, то есть действий, которые производятся в определенной последовательности над числами и переменными величинами.
Например, пусть «a» — это символ, которым я обозначу действие «пройти прямо 1 метр», «b» — «повернуть на 90 градусов налево», «с» — копать вниз на 1 метр, а знак «+» обозначает совершение последующего действия. Тогда указание на место, где закопан доллар, я могу записать в виде формулы: 3а + b + 3с. Этой формулой определены обозначенные символами действия, которые производятся в определенной последовательности.
Формула – наиболее распространенный способ задания функции. Делается запись в виде равенства двух аналитических выражений, в которых участвуют две переменные величины, и по значению одной из них, которую мы принимаем за независимую переменную, мы с помощью вычислений определяем соответствующее значение другой переменной – функции.
Если у, будучи функцией х, задана формулой, то говорят, что эта формула устанавливает функциональную зависимость между у и х, или, попросту, связывают эти две величины.
Аналитический способ задания функции имеет огромные преимущества:
1) сжатость, компактность – не надо рисовать бесконечные таблицы или сложные, выверенные графики.
2) мы можем вычислить значение функции вообще для какого угодно значения независимой переменной. Например, я могу совершенно точно вычислить площадь круга радиусом 3,74322473847 метра. Попробуй сделать это с помощью графика!
3) третье преимущество – которое, наверное, сейчас будет малопонятно – это возможность изучать эту функцию с помощью аппарата математического анализа
Есть и неудобства, довольно очевидные: во-первых, слабая или вообще никакая наглядность, ну и во-вторых необходимость производить вычисления, которые могут быть такими громоздкими, что все преимущества растают без следа.
Думаю, что легко понять, что в определении понятия функции нет такого требования, чтобы при изменении независимой переменной менялась и функция. Главное – чтобы каждому рассматриваемому значению независимой переменной соответствовало определенное значение функции, а уж одно и тоже оно или разные — несущественно.
Вот это – функция?
| х | 1 | 2 | 3 | 4 | 5 |
| у | 1 | 1 | 1 | 1 | 1 |
Да, функция, ведь каждому значению «х» соответствует определенное, пусть и одинаковое, значение «у».
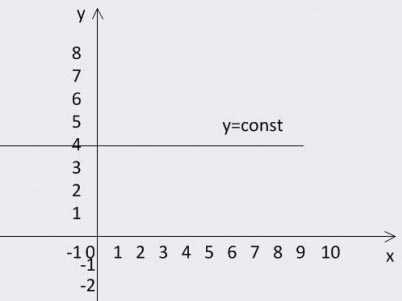
Отсюда следует интересное следствие – даже постоянную величину можно рассматривать как функцию! Ведь достаточно сказать, что любому значению переменной величины x мы ставим в соответствие, скажем, число 4 – вот такое простое правило. И число 4 станет функцией, все значения которой равны четырем при любых значениях независимой переменной х.
Осталось в этой главе ввести еще два простых термина: область определения функции и область значений функции.
«Областью определения функции» называется множество всех значений, которые может принимать переменная х, а «областью значений функции» называют множество всех значений, которые может принимать вычисляемая в соответствии с формулой переменная у.
Так, легко видеть, что в формуле
y = x2
переменная х может принимать любые значения, какие мы захотим – как положительные, так и отрицательные (и также ноль), то есть область определения данной функции – все числа. Между тем y никак не может быть отрицательным числом, так как число, возведенное в квадрат, дает или ноль или положительное число, поэтому «область значений данной функции» — это ноль и положительные числа.
Если мы напишем формулу в виде:
х =√у
то все изменится: теперь x является функцией от y, и это влечет определенные последствия. Во-первых, теперь область определения этой функции — то есть значения, которые может принимать переменная у — ограничена нулем и положительными числами, так как мы же не можем брать квадратный корень из отрицательного числа. А область значений этой функции (то есть значения, которые может принимать переменная х) может принимать любые значения. Например, если у равно 4, то х может быть и положительным числом (+2) и отрицательным (-2), так как и то и другое, возведенное в квадрат, дает 4.
Вернемся еще раз к графику. Функцию, как мы уже поняли, можно задать в виде графика – откладывай на оси абсцисс значения независимой переменной, обозначим ее как х, на оси ординат откладывай соответствующие значения функции, обозначим ее как у — и вот тебе график. Но теперь проведем обратную операцию. Просто возьмем пустую бумагу с осями координат и проведем на ней совершенно произвольную непрерывную линию. Ну линия и линия. Но теперь посмотрим на нее другими глазами. Каждая точка на линии имеет свою абсциссу и ординату. А это и означает, что эта линия является графиком некой функции! Да, любая непрерывная линия на плоскости изображает некоторую функцию, ведь если мы теперь в любом, произвольном месте того же листа бумаги построим оси координат, то теперь любая точка нашей линии будет иметь какую-то абсциссу и какую-то ординату. А это и значит, что имеет место функция.
Любая непрерывная линия является графиком функции. В подобных случаях говорят, что функция «задана графически». В физике и в технике такое происходит сплошь и рядом. Например, на сейсмостанции датчик рисует непрерывную линию сейсмической активности земной коры. Анализируя этот график, мы можем создавать разные теории строения земли. По такому же принципу работает термограф, вычерчивающий график суточной температуры.
Разумеется, задать функцию графически легко — начертил произвольно какую угодно линию, и график готов. Но это совсем не означает, что мы теперь можем легко записать ее и в аналитическом виде, то есть в виде формулы. Более того, как правило это очень сложно — подобрать такую формулу, которая бы описывала произвольно нарисованный график. Этим занимается специальная область математики.
Есть символы, которые используются в формулах чаще всего, и удобно запомнить их. Например, вместо того, чтобы писать «величина у есть некоторая функция независимой переменной величины х», пишут просто:
y = f (x)
Эта запись читается так: «игрек есть функция от икс», или еще проще: «игрек равно эф от икс».
Здесь буква f обозначает уже не величину, не какое-то определенное число, а саму зависимость, то есть закон соответствия между независимой переменной и функцией.
Если я не хочу вдаваться в детальное описание того, как именно площадь круга зависит от его радиуса, а просто хочу указать, что такая зависимость существует, то мне совершенно нет необходимости выписывать точную формулу – достаточно написать:
S = f (r)
Так как и длина окружности (L) – тоже функция ее радиуса, то мы можем написать аналогично:
L= f (r)
Эти записи выглядят совершенно одинаково несмотря на то, что аналитические выражения этих двух функций отличаются друг от друга очень сильно. И это неудобно и может вызывать невольные ошибки, поэтому – если функциональные зависимости отличаются, то математики и физики используют разные буквы, например:
S = f (r) , L= g (r)
Можно для обозначения разных зависимостей использовать одинаковые буквы, но разные индексы к ним:
S = f 1 (r) , L= f 2 (r)
И последнее для этой главы: имея конкретную формулу, которой выражена функция, мы можем вычислить, чему равно значение функции при каком-то конкретном значении независимой переменной. Например, если мы имеем формулу y = x2, то сначала мы подставляем значение переменной (скажем, пусть радиус равняется 3), производим нужные вычисления согласно формуле (возводим 3 в квадрат) и получаем значение функции (9). Это будет называться «частным значением функции». Это можно записать так:
9 = f (3)
bodhi.name
Словарь математических терминов
Словарь математических терминов
Краткий словарь иностранных терминов в математике
От составителей
Перед вами краткий словарь математических терминов. Он представляет собой словарь-справочник для всех, кто интересуется математикой. Но, прежде всего он обращен к школе: как к учителю, так и к учащимся. Такой адресат определяет в принципе и состав его словника, т.е. объясняемые в словаре слова, и принятую в нем форму изложения, значительно более простую и доступную, нежели во всех существующих этимологических словарях.
Т.к. большинство слов современной научной лексики восходит к латыни или еще более древнему греческому языку, в словаре толкуется происхождение основных математических терминов и дается их определение.
Мы постарались собрать почти все математические термины из школьного курса, заимствованные из других языков. Тем более что «математическая этимология» разбросана в небольшом количестве относительно малодоступных книг и привлекает постоянное внимание, невольно прививает интерес к математике, расширяет кругозор, повышает общую культуру речи, позволяет глубже проникнуть в тайны математического языка, лучше понять определения слов.
Но «мир математики велик, а человек мал», так что, конечно, мы отдаем себе отчет в том, что предлагаемая книга отнюдь не свободна от недостатков и упущений. Многие будут пользоваться ею от случая к случаю, снимая с полки только тогда, когда натолкнутся на малопонятный математический термин.
«Моментальная» справка наводится с помощью алфавитного указателя. Как принято в большинстве современных книг по лингвистике, греческие слова мы будем записывать в латинской транскрипции. После основного текста в словаре помещаются таблица возникновения основных математических знаков и список сокращений, употребляемых при толковании этимологии слов.
Е. Половинкина, С. Шакирова
www.mat-analiz.ru
Словарь математических терминов-А
Словарь математических терминов-А
Краткий словарь иностранных терминов в математике
A
Абсцисса (лат. слово abscissa - «отрезанная»). Заимств. из франц. яз. в начале 19 в. Франц. abscisse – из лат. Это одна из декартовых координат точки, обычно первая, обозначаемая буквой x. В современном смысле Т. употреблен впервые немецким ученым Г. Лейбницем (1675).
Аддитивность(лат. слово additivus – «прибавляемый»). Свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части.
Адъюнкта (лат. слово adjunctus – «присоединенный»). Это то же, что и алгебраическое дополнение.
Аксиома (греч. слово axios- ценный; axioma – «принятие положения», «почет», «уважение», «авторитет»). В рус.яз. – с Петровских времен. Это основное положение, самоочевидный принцип. Впервые Т. встречается у Аристотеля. Использовался в книгах Евклида «Начала». Большую роль сыграли работы древнегреческого ученого Архимеда, который сформулировал аксиомы, относящиеся к измерению величин. Вклад в аксиоматику внесли Лобачевский, Паш, Пеано. Логически безупречный список аксиом геометрии был указан немецким математиком Гильбертом на рубеже 19 и 20 вв.
Аксонометрия (от греч. слова akon – «ось» и metrio – «измеряю»). Это один из способов изображения пространственных фигур на плоскости.
Алгебра (араб. слово «ал-джебр». Заимств. В 18 в. из польск. яз.). Это часть математики, развивающаяся в связи с задачей о решении алгебраических уравнений. Т. впервые появляется у выдающегося среднеазиатского математика и астронома 11 века Мухам меда бен-Мусы ал-Хорезми.
Анализ (греч. слово analozis – «решение», «разрешение»). Т. «аналитическая» восходит к Виету, который отвергал слово «алгебра» как варварское, заменяя его словом «анализ».
Аналогия (греч. слово analogia – «соответствие», «сходство»). Это умозаключение по сходству частных свойств, имеющихся у двух математических понятий.
Антилогарифмлат. слово nummerus – «число»). Это число, которое имеет данное табличное значение логарифма, обозначается буквой N.
Антье (франц. слово entiere – «целый»). Это то же, что целая часть действительного числа.
Апофема (греч. слово apothema,apo – «от», «из»; thema – «приложенное», «поставленное»).
1.В правильном многоугольнике апофема – отрезок перпендикуляра, опущенного из его центра на любую из его сторон, а также его длина.
2.В правильной пирамиде апофема – высота любой его боковой грани.
3.В правильной усеченной пирамиде апофема – высота любой ее боковой грани.
Аппликата (лат. слово applicata – «приложенная»). Это одна из декартовых координат точки в пространстве, обычно третья, обозначаемая буквой Z.
Аппроксимация (лат.слово approximo – «приближаюсь»). Замена одних математических объектов другими, в том или ином смысле близкими к исходным.
Аргумент функции (лат. слово argumentum – «предмет», «знак»). Это независимая переменная величина, по значениям которой определяют значения функции.
Арифметика (греч. слово arithmos – «число»). Это наука, изучающая действия над числами. Арифметика возникла в странах Др. Востока, Вавилона, Китае, Индии, Египте. Особый вклад внесли: Анаксагор и Зенон, Евклид, Эратосфен, Диофант, Пифагор, Л. Пизанский и др.
Арктангенс, Арксинус (приставка «арк»- лат. слово arcus – «лук», «дуга»). Arcsin и arctg появляются в 1772 году в работах венского математика Шеффера и известного французского ученого Ж.Л. Лагранжа, хотя несколько ранее их уже рассматривал Д. Бернулли, но который употреблял другую символику.
Асимметрия (греч. слово asymmetria – «несоразмерность»). Это отсутствие или нарушение симметрии.
Асимптота (греч. слово asymptotes – «несовпадающий»). Это прямая, к которой неограниченно приближаются точки некоторой кривой по мере того, как эти точки удаляются в бесконечность.
Астроида (греч. слово astron – «звезда»). Алгебраическая кривая.
Ассоциативность (лат. слово associatio – «соединение»). Сочетательный закон чисел. Т. введен У.Гамильтоном (1843).
www.mat-analiz.ru
Математические термины | Сайт учителя математики Желтышевой Валерии Валерьевны
Абсцисса (лат. слово abscissa — «отрезанная»). Заимств. из франц. яз. в начале 19 в. Франц. abscisse – из лат. Это одна из декартовых координат точки, обычно первая, обозначаемая буквой x. В современном смысле Т. употреблен впервые немецким ученым Г. Лейбницем (1675).
Аддитивность (лат. слово additivus – «прибавляемый»). Свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям при любом разбиении объекта на части.
Адъюнкта (лат. слово adjunctus – «присоединенный»). Это то же, что и алгебраическое дополнение.
Аксиома (греч. слово axios- ценный; axioma – «принятие положения», «почет», «уважение», «авторитет»). В рус.яз. – с Петровских времен. Это основное положение, самоочевидный принцип. Впервые Т. встречается у Аристотеля. Использовался в книгах Евклида «Начала». Большую роль сыграли работы древнегреческого ученого Архимеда, который сформулировал аксиомы, относящиеся к измерению величин. Вклад в аксиоматику внесли Лобачевский, Паш, Пеано. Логически безупречный список аксиом геометрии был указан немецким математиком Гильбертом на рубеже 19 и 20 вв.
Аксонометрия (от греч. слова akon – «ось» и metrio – «измеряю»). Это один из способов изображения пространственных фигур на плоскости.
Алгебра (араб. слово «ал-джебр». Заимств. В 18 в. из польск. яз.). Это часть математики, развивающаяся в связи с задачей о решении алгебраических уравнений. Т. впервые появляется у выдающегося среднеазиатского математика и астронома 11 века Мухам меда бен-Мусы ал-Хорезми.
Анализ (греч. слово analozis – «решение», «разрешение»). Т. «аналитическая» восходит к Виету, который отвергал слово «алгебра» как варварское, заменяя его словом «анализ».
Аналогия (греч. слово analogia – «соответствие», «сходство»). Это умозаключение по сходству частных свойств, имеющихся у двух математических понятий.
Антилогарифмлат. слово nummerus – «число»). Это число, которое имеет данное табличное значение логарифма, обозначается буквой N.
Антье (франц. слово entiere – «целый»). Это то же, что целая часть действительного числа.
Апофема (греч. слово apothema,apo – «от», «из»; thema – «приложенное», «поставленное»).
1.В правильном многоугольнике апофема – отрезок перпендикуляра, опущенного из его центра на любую из его сторон, а также его длина.
2.В правильной пирамиде апофема – высота любой его боковой грани.
3.В правильной усеченной пирамиде апофема – высота любой ее боковой грани.
Аппликата (лат. слово applicata – «приложенная»). Это одна из декартовых координат точки в пространстве, обычно третья, обозначаемая буквой Z.
Аппроксимация (лат.слово approximo – «приближаюсь»). Замена одних математических объектов другими, в том или ином смысле близкими к исходным.
Аргумент функции (лат. слово argumentum – «предмет», «знак»). Это независимая переменная величина, по значениям которой определяют значения функции.
Арифметика (греч. слово arithmos – «число»). Это наука, изучающая действия над числами. Арифметика возникла в странах Др. Востока, Вавилона, Китае, Индии, Египте. Особый вклад внесли: Анаксагор и Зенон, Евклид, Эратосфен, Диофант, Пифагор, Л. Пизанский и др.
Арктангенс, Арксинус (приставка «арк»- лат. слово arcus – «лук», «дуга»). Arcsin и arctg появляются в 1772 году в работах венского математика Шеффера и известного французского ученого Ж.Л. Лагранжа, хотя несколько ранее их уже рассматривал Д. Бернулли, но который употреблял другую символику.
Асимметрия (греч. слово asymmetria – «несоразмерность»). Это отсутствие или нарушение симметрии.
Асимптота (греч. слово asymptotes – «несовпадающий»). Это прямая, к которой неограниченно приближаются точки некоторой кривой по мере того, как эти точки удаляются в бесконечность.
Астроида (греч. слово astron – «звезда»). Алгебраическая кривая.
Ассоциативность (лат. слово associatio – «соединение»). Сочетательный закон чисел. Т. введен У.Гамильтоном (1843).
Биллион (франц. слово billion, или миллиард – milliard). Это тысяча миллионов, число изображаемое единицей с 9 нулями, т.е. число 10 9 . В некоторых странах биллионом называют число, равное 10 12.
Бином лат. слова bi – «двойной», nomen – «имя». Это сумма или разность двух чисел или алгебраических выражений, называемых членами бинома.
Биссектриса (лат. слова bis – «дважды» и sectrix –«секущая»). Заимств. В 19 в. из франц. яз. где bissectrice – восходит к лат. словосочетанию. Это прямая, проходящая через вершину угла и делящая его пополам.
Вектор (лат. слово vector – «несущий», «носитель»). Это направленный отрезок прямой, у которой один конец называют началом вектора, другой конец – концом вектора. Этот термин ввел ирландский ученый У. Гамильтон (1845).
Вертикальные углы (лат. слова verticalis – «вершинный»). Это пары углов с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
Гексаэдр (греч. слова geks – «шесть» и edra – «грань»). Это шестигранник. Этот Т. приписывают древнегреческому ученому Паппу Александрийскому (3 век).
Геометрия (греч. слова geо – «Земля» и metreo – «измеряю»). Др.-рус. заимств. из греч.яз. Часть математики, изучающая пространственные отношения и формы. Т. появился в 5 веке до н.э. в Египте, Вавилоне.
Гипербола (греч. слово hyperballo – «прохожу через что-либо»). Заимств. в 18 в. из лат. яз. Это незамкнутая кривая из двух неограниченно простирающихся ветвей. Т.ввел древнегреческий ученый Апполоний Пермский.
Гипотенуза (греч.слово gyipotenusa – «стягивающая»). Замств. из лат. яз. в 18 в., в котором hypotenusa – от греч. сторона прямоугольного треугольника, лежащая против прямого угла. Древнегреческий ученый Евклид (3 век до н.э.) вместо этого термина писал, «сторона, которая стягивает прямой угол».
Гипоциклоида (греч. слово gipo – «под», «внизу»). Кривая, которую при этом описывает точка окружности.
Гониометрия (лат. слово gonio – «угол»). Это учение о «тригонометрических» функциях. Однако это название не привилось.
Гомотетия (греч. слово homos- «равный», «одинаковый», thetos — «расположенный»). Это расположение подобных между собой фигур, при котором прямые, соединяющие соответствующие друг другу точки фигур, пересекаются в одной и той же точке, называемой центром гомотетии.
Градус (лат. слово gradus – «шаг», «ступень»). Единица измерения плоского угла, равная 1/90 части прямого угла. Измерение углов в градусах появилось более 3 лет назад в Вавилоне. Обозначения, напоминающие современные, использовались древнегреческими ученым Птолемеем.
График (греч. слово graphikos- «начертанный»). Это график функции – кривая на плоскости, изображаемая зависимость функции от аргумента.
Дедукция (лат. слово deductio-«выведение»). Это форма мышления, посредством которой утверждение выводится чисто логически (по правилам логики) из некоторых данных утверждений – посылок.
Деференты (лат. слово defero-«несу», «перемещаю»). Это окружность, по которой вращаются эпициклоиды каждой планеты. У Птолемея планеты вращаются по окружностям – эпициклам, а центры эпициклов каждой планеты вращаются вокруг Земли по большим окружностям – деферентам.
Диагональ (греч. слово dia – «через» и gonium – «угол»). Это отрезок прямой, соединяющий две вершины многоугольника, не лежащие на одной стороне. Т. встречается у древнегреческого ученого Евклида (3 век до н.э.).
Диаметр (греч. слово diametros – «поперечник», «насквозь», «измеряющий» и слово dia – «между», «сквозь»). Т. «деление» в русском языке впервые встречаются у Л.Ф.Магницкий.
Директриса (лат. слово directrix – «направляющий»).
Дискретность (лат. слово discretus – «разделенный», «прерывистый»). Это прерывность; противопоставляется непрерывности.
Дискриминант (лат. слово discriminans- «различающий», «разделяющий»). Это составленное из величин, определенных заданную функцию, выражение, обращением которого в нуль характеризуется то или иное отклонение функции от нормы.
Дистрибутивность (лат. слово distributivus – «распределительный»). Распределительный закон, связывающий сложение и умножение чисел. Т. ввел франц. ученый Ф. Сервуа (1815 г.).
Дифференциал (лат. слово differento- «разность»). Это одно из основных понятий математического анализа. Этот Т. встречается у немецкого ученого Г. Лейбница в 1675 г. (опубликовано в 1684г.).
Дихотомия (греч.слово dichotomia – «разделение надвое»). Способ классификации.
Додекаэдр (греч. слова dodeka – «двенадцать» и edra – «основание»). Это один из пяти правильных многогранников. Т. впервые встречается у древнегреческого ученого Теэтет (4 век до н.э.).
Знаменатель — число, показывающее размеры долей единицы, из которых составлена дробь. Впервые встречается у византийского ученого Максима Плануда (конец 13 века).
Изоморфизм (греч. слова isos – «равный» и morfe – «вид», «форма»). Это понятие современной математики, уточняющее широко распространенное понятие аналогии, модели. Т. был введен в середине 17 века.
Икосаэдр (греч. слова eicosi – «двадцать» и edra – основание). Один из пяти правильных многогранников; имеет 20 треугольных граней, 30 ребер и 12 вершин. Т. дан Теэтетом, который и открыл его (4 век до н.э.).
Инвариантность(лат. слова in — «отрицание» и varians — «изменяющийся»). Это неизменность какой-либо величины по отношению к преобразованиям координат. Т. введен англ. ученым Дж. Сильвестром (1851).
Индукция (лат. слово inductio – «наведение»). Один из методов доказательства математических утверждений. Этот метод впервые появляется у Паскаля.
Индекс (лат. слово index – «указатель». Заимств. в начале 18 в. из лат. яз.). Числовой или буквенный указатель, которым снабжаются математические выражения для того, чтобы отличать их друг от друга.
Интеграл (лат. слово integro – «восстанавливать» или integer – «целый»). Заимств. во второй половине 18 в. из франц. яз. на базе лат. integralis – «целый», «полный». Одно из основных понятий математического анализа, возникшее в связи потребностью измерять площади, объемы, отыскивать функции по их производным. Обычно эти концепции интеграла связывают с Ньютоном и Лейбницем. Впервые это слово употребил в печати швец. Ученый Я. Бернулли (1690 г.). Знак ? — стилизованная буква S от лат. слова summa – «сумма». Впервые появился у Г. В. Лейбница.
Интервал (лат. слово intervallum – «промежуток», «расстояние»). Множество действительных чисел, удовлетворяющее неравенству a < x <b.
Иррациональное число (т. слово irrationalis – «неразумный»). Число, не являющееся рациональным. Т. ввел немецк. ученый М.Штифель (1544). Строгая теория иррациональных чисел была построена во 2-ой половине 19 века.
Итерация (ат. слово iteratio – «повторение»). Результат повторного применения какой-либо математической операции. </b.
Калькулятор — немецк. слово kalkulator восходит к лат. слову calculator – «считать». Заимств. в конце 18 в. из немец. яз. Портативное вычислительное устройство.
Каноническое разложение — греч. слово canon – «правило», «норма».
Касательная — лат.слово tangens – «касающийся». Семантическая калька конца 18 века.
Катет — лат. слово katetos – «отвес». Сторона прямоугольного треугольника, прилежащая к прямому углу. Т. впервые встречается в форме «катетус» в «Арифметике» Магницкого 1703 года, но уже во втором десятилетии 18 века получает распространение современная форма.
Квадрат — лат.слово quadratus – «четырехугольный» (от guattuor — «четыре»). Прямоугольник, у которого все стороны равны, или, что равносильно, ромб, у которого все углы равны.
Кватернионы — лат. слово quaterni – «по четыре». Система чисел, возникшая при попытках найти обобщение комплексных чисел. Т. предложен англ. ученым Гамильтоном (1843).
Квинтиллион — франц.слово quintillion. Число, изображаемое единицей с 18 нулями. Заимствовано в конце 19 века.
Коллинеарность — лат.слово con, com – «вместе» и linea — «линия». Расположенность на одной линии (прямой). Т. ввел америк. ученый Дж.Гиббс; впрочем, это понятие встречалось ранее у У. Гамильтона (1843).
Комбинаторика — лат.слово combinare – «соединять». Раздел математики, в котором изучаются различные соединения и размещения, связанные с подсчетом комбинаций из элементов данного конечного множества.
Компланарность — лат.слова con, com – «вместе» и planum – «плоскость». Расположение в одной плоскости. Т. впервые встречается у Я.Бернулли; впрочем, это понятие встречалось ранее у У.Гамильтона (1843).
Коммутативность — позднелат. слово commutativus – «меняющийся». Свойство сложения и умножения чисел, выражаемое тождествами: a+b=b+a , ab=ba.
Конгруэнтность — лат. слово congruens – «соразмерный». Т., употребляемый для обозначения равенства отрезков, углов, треугольников и др.
Константа — лат.слово constans–«постоянный», «неизменный». Постоянная величина при рассмотрении математических и др. процессов.
Конус — греч. слово konos – «кегля», «шишка», «верхушка шлема». Тело, ограниченное одной полостью конической поверхности и пересекающей эту полость плоскостью, перпендикулярной ее оси. Т. получил современный смысл у Аристарха, Евклида, Архимеда.
Конфигурация — лат. слово со – «вместе» и figura — «вид». Расположение фигур.
Конхоида — греч. слово conchoides – «подобная раковине мидии». Алгебраическая кривая. Ввел Никомед из Александрии (2 век до н.э.).
Координаты — лат.слово со – «вместе» и ordinates — «определенный». Числа, взятые в определенном порядке, определяющие положение точки на линии, плоскости, пространстве. Т. ввел Г. Лейбниц (1692).
Косеканс — лат. слово cosecans. Одна из тригонометрических функций.
Косинус — лат.слово complementi sinus, complementus – «дополнение», sinus – «впадина». Заимств. в конце 18 в. из языка ученой латыни. Одна из тригонометрических функций, обозначаемая cos. Ввел Л.Эйлер в 1748 году.
Котангенс — лат. слово complementi tangens: complementus – «дополнение» или от лат. слова cotangere – «соприкасаться». Во второй половине 18 в. из языка научной латыни. Одна из тригонометрических функций, обозначается ctg.
Коэффициент — лат. слово со – «вместе» и efficiens – «производящий». Множитель, обычно выражаемый цифрами. Т. ввел Виет.
Куб — греч. слово kubos – «игральная кость». Заимств. в конце 18 в. из ученой латыни. Один из правильных многогранников; имеет 6 квадратных граней, 12 ребер, 8 вершин. Название введено пифагорейцами, затем встречается у Евклида (3 век до н.э.).
Лемма — греч. слово lemma – «допущение». Это вспомогательное предложение, употребляемое при доказательствах других утверждений. Т. введен древнегреческими геометрами; особенно часто встречается у Архимеда.
Лемниската — греч. слово lemniscatus – «украшенный лентами». Алгебраическая кривая. Изобрел Бернулли.
Линия — лат. слово linea – «лен», «нить»,«шнур», «веревка». Один из основных геометрических образов. Представлением о ней может служить нить или образ, описываемый движением точки в плоскости или пространстве.
Логарифм — греч. слово logos – «отношение» и arithmos – «число». Заимств. в 18 в. из франц. яз., где logarithme — англ. logarithmus – образовано сложением греч. слов. Показатель степени m, в которую необходимо возвести a, чтобы получить N.Т. предложил Дж. Непер.
Максимум — лат.слово maximum – «наибольшее». Заимств. во второй половине 19 в. из лат. яз. Наибольшее значение функции на множестве определения функции.
Мантисса — лат. слово mantissa – «прибавка». Это дробная часть десятичного логарифма. Т. был предложен российским математиком Л. Эйлером (1748).
Масштаб — немецк. слово mas – «мера» и stab – палка». Это отношение длины линии на чертеже к длине соответствующей линии в натуре.
Математика — греч. слово matematike от греч.слова matema – «знание», «наука». Заимств. в начале 18 в. из лат. яз., где mathematica – греч. Наука о количественных отношениях и пространственных формах действительного мира.
Матрица — лат. слово matrix – «матка», «источник», «начало». Это прямоугольная таблица, образованная из некоторого множества и состоящая из строк и столбцов. Впервые Т. появился у У. Гамильтона и ученых А. Кэли и Дж. Сильвестра в сер. 19 века. Современное обозначение – две вертик. черточки — ввел А. Кэли (1841).
Медиана (треуг-ка) — лат. слово medianus – «средний». Это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Метр — франц. слово metre – «палка для измерения» или греч. слово metron – «мера». Заимств. в 18 в. из франц. яз., где metre – греч. Это основная единица длины. Она появилась на свет 2 века назад. Метр был «рожден» Великой французской революцией в 1791 году.
Метрика — греч.слово metrike < metron – «мера», «размер». Это правило определения расстояния между любыми двумя точками данного пространства.
Миллион — итал. слово millione – «тысячище». Заимств. в Петровскую эпоху из франц. яз., где million – итал. Число, записанное с шестью нулями. Т. придумал Марко Поло.
Миллиард — франц. слово mille – «тысяча». Заимств. в 19 в. из франц. яз., где milliard – суф. Производное от mille – «тысяча».
Минимум — лат.слово minimum – «наименьшее». Наименьшее значение функции на множестве определения функции.
Минус — лат.слово minus – «менее». Это математический знак в виде горизонтальной черты, употребляемый для обозначения отрицательных чисел и действия вычитания. Введен в науку Видманом в 1489 году.
Минута — лат. слово minutus – «мелкий», «уменьшенный». Заимств. в начале 18 в. из франц. яз., где minute – лат. Это единица измерения плоских углов, равная 1/60 градуса.
Модуль — лат. слово modulus – «мера», «величина». Это абсолютная величина действительного числа. Т. ввел Р.Котс, ученик И. Ньютона. Знак модуля введен в 19 веке К.Вейерштрассом.
Мультипликативность — лат. слово multiplicatio – «умножение». Это свойство функции Эйлера.
Норма — лат.слово norma – «правило», «образец». Обобщение понятия абсолютной величины числа. Знак «нормы» ввел немецк.ученый Э.Шмидт (1908).
Нуль — лат слово nullum–«ничто», «никакой». Первоначально Т. обозначал отсутствие числа. Обозначение нуля появилось около середины первого тысячелетия до н.э.
Нумерация — лат. слово numero – «считаю». Это счисление или совокупность приемов наименования и обозначения чисел.
Овал — лат. слово ovaum – «яйцо».Заимств. в 18 в. из франц., где ovale – лат. Это замкнутая выпуклая плоская фигура
Окружность греч. слово periferia – «периферия», «окружность». Это множество точек плоскости, находящихся на данном расстоянии от данной точки, лежащей в той же плоскости и называемой ее центром.
Октаэдр — греч. слова okto – «восемь» и edra – «основание». Это один из пяти правильных многогранников; имеет 8 треугольных граней, 12 ребер и 6 вершин. Этот Т. дан древнегреческим ученым Теэтетом (4 век до н.э), который впервые и построил октаэдр.
Ордината — лат.слово ordinatum – «по порядку». Одна из декартовых координат точки, обычно вторая, обозначаемая буквой y. Как одна из декартовых координат точки, этот Т. употреблен немецк. ученым Г.Лейбницем (1694 г.).
Орт — греч. слово ortos – «прямой». То же, что единичный вектор, длина которого принята равной единице. Т. ввел англ. ученый О.Хевисайд (1892 г.).
Ортогональность — греч. слово ortogonios – «прямоугольный». Обобщение понятие перпендикулярности. Встречается у древнегреческого ученого Евклида (3 век до н.э.).
Парабола — греч. слово parabole – «приложение».Это нецентральная линия второго порядка, состоящая из одной бесконечной ветви, симметричной относительно оси. Т. ввел древнегреческий ученый Аполлоний Пергский, рассматривавший параболу как одно из конических сечений.
Параллелепипед — греч.слово parallelos- «параллельный» и epipedos – «поверхность». Это шестигранник, все грани которого – параллелограммы. Т. встречался у древнегреческих ученых Евклида и Герона.
Параллелограмм — греч.слова parallelos – «параллельный» и gramma – «линия», «черта». Это четырехугольник, у которого противоположные стороны попарно параллельны. Т. начал употреблять Евклид.
Параллельность — parallelos – «рядом идущий». До Евклида Т. употреблялся в школе Пифагора.
Параметр — греч.слово parametros – «отмеривающий». Это вспомогательная переменная, входящая в формулы и выражения.
Периметр — греч.слово peri – «вокруг», «около» и metreo – «измеряю». Т. встречается у древнегреческих ученых Архимеда (3 век до н.э.), Герона (1 век до н.э.), Паппа (3 век).
Перпендикуляр — лат.слово perpendicularis – «отвесный». Это прямая, пересекающая данную прямую (плоскость) под прямым углом. Т. был образован в средние века.
Пирамида — греч.слово pyramis, кот. произошло от егип.слова permeous – «боковое ребро сооружения» или от pyros –«пшеница», или от pyra – «огонь». Заимств. из ст.-сл. яз. Это многогранник, одна из граней которого – плоский многоугольник, а остальные грани – треугольники с общей вершиной, не лежащей в плоскости основания.
Площадь — греч. слово plateia – «широкая». Происхождение неясно. Некоторые ученые считают заимств. из ст.-сл. Другие толкуют как исконно русское.
Планиметрия — лат.слово planum – «плоскость» и metreo – «измеряю». Это часть элементарной геометрии, в которой изучаются свойства фигур, лежащих в плоскости. Т. встречается у древнегреч. ученого Евклида (4 век до н.э.).
Плюс — лат.слово plus – «больше». Это знак для обозначения действия сложения, а также для обозначения положительности чисел. Знак ввел чешский ученый Я. Видман (1489 г.).
Полином — греч.слово polis – «многочисленный», «обширный» и лат.слово nomen – «имя». Это то же, что многочлен, т.е. сумма некоторого числа одночленов.
Потенцирование — немецк.слово potenzieren – «возводить в степень». Действие, заключающееся в нахождении числа по данному логарифму.
Предел — лат.слово limes – «граница». Это одно из основных понятий математики, означающее, что некоторая переменная величина в рассматриваемом процессе ее изменения неограниченно приближается к определенному постоянному значению. Т. ввел Ньютон, а употребляемый ныне символ lim (3 первые буквы от limes) – франц.ученый С.Люилье (1786 г.). Выражение lim первым записал У.Гамильтон (1853 г.).
Призма — греч. слово prisma – «отпиленный кусок». Это многогранник, две грани которого – равные n-угольники, называемые основаниями призмы, а остальные грани – боковые. Т. встречается уже в 3 веке до н.э. у древнегреч. ученых Евклида и Архимеда.
Пример — греч.слово primus – «первый». Задача с числами. Т. изобрели греческие математики.
Производная — франц.слово derivee. Ввел Ж.Лагранж в 1797 году.
Проекция — лат.слово projectio – «бросание вперед». Это способ изображения плоской или пространственной фигуры.
Пропорция — лат.слово proportio – «соотношение». Это равенство между двумя отношениями четырех величин.
Процент — лат.слово pro centum — «со ста». Идея процента возникла в Вавилоне.
Постулат — лат.слово postulatum – «требование». Употребляемое иногда название для аксиом математической теории
Радиан — лат.слово radius – «спица», «луч». Это единица измерения углов. Первое издание, содержащее этот термин, появилось в 1873 году в Англии.
Радикал — лат. слово radix – «корень», radicalis – «коренной». Современный знак ? впервые появился в книге Р.Декарта «Геометрия», изданной в 1637 г. Этот знак состоит из двух частей: модифицированной буквы r и черты, заменявшей ранее скобки. Индийцы называли «мула», арабы – «джизр», европейцы – «радикс».
Радиус — лат слово radius – «спица в колесе». Заимств. в Петровскую эпоху из лат. яз. Это отрезок, соединяющий центр окружности с какой-либо ее точкой, а также длина этого отрезка. В древности Т. не было, он встречается впервые в 1569 г. у франц. ученого П. Раме, затем у Ф.Виета и становится общепринятым в конце 17 века.
Рекуррентный — лат.слово recurrere – «возвращаться назад». Это возвратное движение в математике.
Ромб — греч.слово rombos – «бубен». Это четырехугольник, у которого все стороны равны. Т. употребляется у древнегреческих ученых Герона (1 век до н.э.), Паппа (2-ая половина 3 века).
Рулетты — франц.слово roulette – «колесико», «сравните», «рулетка», «руль». Это кривые. Т. придумали франц. математики, изучавшие свойство кривых.
Сегмент — лат.слово segmentum – «отрезок», «полоса». Это часть круга, ограниченная дугой граничной окружности и хордой, соединяющей концы этой дуги.
Секанс — лат.слово secans – «секущая». Это одна из тригонометрических функций. Обозначается sec.
Секстиллион — франц.слово sextillion. Число, изображаемое с 21 нулем, т.е. число 1021.
Сектор — лат.слово seco – «режу». Это часть круга, ограниченная дугой его граничной окружности и двумя ее радиусами, соединяющими концы дуги с центром круга.
Секунда — лат.слово secunda – «вторая». Это единица измерения плоских углов, равная 1/3600 градуса или 1/60 минуты.
Сигнум — лат.слово signum – «знак». Это функция действительного аргумента.
Симметрия — греч.слово simmetria – «соразмерность». Свойство формы или расположения фигур симметрично.
Синус — лат. sinus –«изгиб», «кривизна», «пазуха». Это одна из тригонометрических функций. В 4-5 вв. называли «ардхаджива» (ардха – половина, джива – тетива лука). Арабскими математиками в 9 в. слово «джайб» — выпуклость. При переводе арабских математических текстов в 12 в. Т. был заменен «синусом». Современное обозначение sin ввел российский ученый Эйлер (1748 г.).
Скаляр — лат.слово scalaris – «ступенчатый». Это величина, каждое значение которой выражается одним числом. Этот Т. ввел ирландский ученый У.Гамильтон (1843 г.).
Спираль — греч.слово speria – «виток». Это плоская кривая, которая обычно обходит вокруг одной (или нескольких) точки, приближаясь или удаляясь от нее.
Стереометрия — греч. слова stereos – «объемный» и metreo – «измеряю». Это часть элементарной геометрии, в которой изучаются пространственные фигуры.
Сумма — лат.слово summa – «итог», «общее количество». Результат сложения. Знак ? (греч. буква «сигма») ввел российский ученый Л.Эйлер (1755 г.).
Сфера — греч. слово sfaira – «шар», «мяч». Это замкнутая поверхность, получаемая вращением полуокружности вокруг прямой, содержащей стягивающий ее диаметр. Т.встречается у древнегреческих ученых Платона, Аристотеля.
Тангенс — лат.слово tanger – «касаться». Одна из тригонометр. функций. Т. введен в 10 веке арабским математиком Абу-л-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Обозначение tg ввел российский ученый Л.Эйлер.
Теорема — греч.слово tereo – «исследую». Это математическое утверждение, истинность которого установлена путем доказательства. Т. употребляется еще Архимедом.
Тетраэдр — греч.слова tetra – «четыре» и edra – «основание». Один из пяти правильных многранников; имеет 4 треугольные грани, 6 ребер и 4 вершины. По-видимому, Т. впервые употреблен древнегреческим ученым Евклидом (3 век до н.э.).
Топология — греч.слово topos – «место». Ветвь геометрии, изучающая свойства геометрических фигур, связанных с их взаимным расположением. Так считали Эйлер, Гаусс, Риман, что Т. Лейбница относится именно к этой ветви геометрии. Во второй половине прошлого столетия в новую область математики, она получила название топологии.
Точка — русс. слово «ткнуть» как бы результат мгновенного прикосновения, укола. Н.И.Лобачевский, впрочем, считал, что Т. происходит от глагола «точить» — как результат прикосновения острия отточенного пера. Одно из основных понятий геометрии.
Трактриса — лат.слово tractus – «вытянутый». Плоская трансцендентная кривая.
Транспозиция — лат.слово transpositio – «перестановка». В комбинаторике перестановка элементов данной совокупности, при которой меняются местами 2 элемента.
Транспортир — лат. слово transortare – «переносить», «перекладывать». Приспособление для построения и измерения углов на чертеже.
Трансцендентный — лат.слово transcendens –«выходящий за пределы», «переходящий». Его впервые употребил немецк.ученый Г.Лейбниц (1686 г).
Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Т. встречается впервые у древнегреческого ученого Посидония (2 век до н.э.).
Триангулированная — лат.слово triangulum – «треугольник».
Тригонометрия — греч.слова trigonon – «треугольник» и metreo –«измеряю». Заимств. в 18 в. из ученой латыни. Раздел геометрии, в котором изучаются тригонометрические функции и их приложения к геометрии. Т. впервые встречается в заглавии книги немецкого ученого Б.Титиска (1595 г.).
Триллион — франц. слово trillion. Заимств. в 18 в. из франц. яз. Число с 12 нулями, т.е. 1012.
Трисекция — угла лат.слова tri – «три» и section – «разрезание», «рассечение». Задача о разделении угла на три равные части.
Трохоида — греч. слово trochoeides – «колесообразный», «круглый». Плоская трансцендентная кривая.
Угол — лат.слово angulus – «угол». Геометрическая фигура, состоящая из двух лучей с общим началом.
Уникурсальный — лат. слова unus – «один», cursus – «путь». Маршрут обхода всех ребер построенного графа, при котором ни одно ребро не проходит дважды.
Факториал (k) — лат.слово factor – «множитель». Впервые появился у французского математика Луи Арбогаста. Обозначение k ввел немецк. математик Кретьен Крамп.
Фигура — лат.слово figura – «внешний вид», «образ». Т. применяемый к разнообразным множествам точек.
Фокус — лат.слово focus – «огонь», «очаг». Расстояние до данной точки. Арабы называли параболу «зажигательным зеркалом», а точку, в которой собираются солнечные лучи – «местом зажигания». Кеплер в «Оптической астрономии» перевел этот Т. словом «фокус».
Формула — лат. слово formula – «форма», «правило». Это комбинация математических знаков, выражающая какое-либо предложение.
Функция — лат. слово functio – «исполнение», «совершение». Одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Т. впервые появляется в 1692 г. у немецк. ученого Г.Лейбница притом не в современном понимании. Т., близкий к современному встречается у швейцарского ученого И.Бернулли (1718 г.). Обозначение функции f(x) ввел российский ученый Л.Эйлер (1734 г.).
Характеристика — греч.слово character – «признак», «особенность». Целая часть десятичного логарифма. Т. был предложен австрийским ученым Г. Бригсом (1624 г.).
Хорда — греч. слово horde – «струна», «тетива». Отрезок, соединяющий две точки окружности.
Центр — лат. слово centrum – «острие ножки циркуля», «колющее орудие». Заимств. в 18 в. из лат. Середина чего-либо, например круга.
Циклоида — греч. слово kykloeides – «кругообразный». Кривая, которую описывает отмеченная точка окружности, катящяяся без скольжения по прямой.
Цилиндр — греч. слово kilindros – «валик», «каток». Заимств. в 18 в. из нем. яз., где zilinder – лат., но восходящее к греч. kylindros. Это тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, перпендикулярными ее оси. Т. встречается у древнегреческих ученых Аристарха, Евклида.
Циркуль — лат. слово circulus – «круг», «обод». Заимств. в первой трети 19 в. из лат. яз. Прибор для вычерчивания дуг, окружностей, линейных измерений.
Циссоида — греч. слово kissoeides – «плющевидный». Алгебраическая кривая. Изобрел греческий математик Диоглес (2 век до н.э.).
Цифры — лат.слова cifra – «цифра», происходящего от арабск.слова «сифр», означающего «нуль».
Числитель — число, показывающее из скольких частей составлена дробь. Т. впервые встречается у византийского ученого Максима Плануда (конец 13 века).
Число ? — (от нач. буквы греч. слова perimetron – «окружность», «преиферия»). Отношение длины окружности к ее диаметру. Впервые появилось у У.Джонса (1706 г.). Стало общепринятым после 1736 года. ? = 3,141592653589793238462…
Шкала — лат.слово scalae – «ступень». Последовательность чисел, служащая для количественной оценки каких-либо величин.
Эвольвента — лат.слово evolvens – «разворачивающий». Развертка кривой.
Экспонента — лат.слово exponentis – «показывающий». То же, что и экспоненциальная функция. Т. ввел немецкий ученый Г.Лейбниц (1679, 1692).
Экстраполирование — лат.слова extra – «сверх» и polio – «приглаживаю», «выправляю». Продолжение функции за пределы ее области определения, при котором продолженная функция принадлежит заданному классу.
Экстремум — лат.слово exstremum – «крайнее». Это общее название максимума и минимума функции.
Эксцентриситет — лат.слова ex – «из», «от» и centrum – «центр». Число, равное отношению расстояния от точки конического сечения до фокуса к расстоянию от этой точки до соответственной директрисы.
Эллипс — греч. слова ellipsis – «недостаток». Это овальная кривая. Т. ввел древнегреческий ученый Апполоний Пергский (260-190 вв. до н.э.).
Энтропия — греч.слово entropia- «поворот», «превращение».
Эпициклоида — греч.слова epi – «над», «на» и kykloeides – «кругообразный». Это плоская кривая, описываемая точкой окружности.
confetti-matematika.ru
Словарь математических терминов (буквы Н — Я)
Матема́тика (др.-греч. μᾰθημᾰτικά < др.-греч. μάθημα — изучение, наука) — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов. Математические объекты создаются путём идеализации свойств реальных или других математических объектов и записи этих свойств на формальном языке. Математика не относится к естественным наукам, но широко используется в них как для точной формулировки их содержания, так и для получения новых результатов. Математика — фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную взаимосвязь и способствует нахождению самых общих законов природы.
Представляем вашему вниманию словарь математических терминов.
Норма — лат.слово norma – «правило», «образец». Обобщение понятия абсолютной величины числа. Знак «нормы» ввел немецк.ученый Э.Шмидт (1908).
Нуль — лат слово nullum–«ничто», «никакой». Первоначально Т. обозначал отсутствие числа. Обозначение нуля появилось около середины первого тысячелетия до н.э.
Нумерация — лат. слово numero – «считаю». Это счисление или совокупность приемов наименования и обозначения чисел.
Овал — лат. слово ovaum – «яйцо».Заимств. в 18 в. из франц., где ovale – лат. Это замкнутая выпуклая плоская фигура
Окружность (греч. слово periferia – «периферия», «окружность») множество точек плоскости, находящихся на данном расстоянии от данной точки, лежащей в той же плоскости и называемой ее центром.
Октаэдр — греч. слова okto – «восемь» и edra – «основание». Это один из пяти правильных многогранников; имеет 8 треугольных граней, 12 ребер и 6 вершин. Этот Т. дан древнегреческим ученым Теэтетом (4 век до н.э), который впервые и построил октаэдр.
Ордината — лат.слово ordinatum – «по порядку». Одна из декартовых координат точки, обычно вторая, обозначаемая буквой y. Как одна из декартовых координат точки, этот Т. употреблен немецк. ученым Г.Лейбницем (1694 г.).
Орт — греч. слово ortos – «прямой». То же, что единичный вектор, длина которого принята равной единице. Т. ввел англ. ученый О.Хевисайд (1892 г.).
Ортогональность — греч. слово ortogonios – «прямоугольный». Обобщение понятие перпендикулярности. Встречается у древнегреческого ученого Евклида (3 век до н.э.).
Парабола — греч. слово parabole – «приложение».Это нецентральная линия второго порядка, состоящая из одной бесконечной ветви, симметричной относительно оси. Т. ввел древнегреческий ученый Аполлоний Пергский, рассматривавший параболу как одно из конических сечений.
Параллелепипед — греч.слово parallelos- «параллельный» и epipedos – «поверхность». Это шестигранник, все грани которого – параллелограммы. Т. встречался у древнегреческих ученых Евклида и Герона.
Параллелограмм — греч.слова parallelos – «параллельный» и gramma – «линия», «черта». Это четырехугольник, у которого противоположные стороны попарно параллельны. Т. начал употреблять Евклид.
Параллельность — parallelos – «рядом идущий». До Евклида Т. употреблялся в школе Пифагора.
Параметр — греч.слово parametros – «отмеривающий». Это вспомогательная переменная, входящая в формулы и выражения.
Периметр — греч.слово peri – «вокруг», «около» и metreo – «измеряю». Т. встречается у древнегреческих ученых Архимеда (3 век до н.э.), Герона (1 век до н.э.), Паппа (3 век).
Перпендикуляр — лат.слово perpendicularis – «отвесный». Это прямая, пересекающая данную прямую (плоскость) под прямым углом. Т. был образован в средние века.
Пирамида — греч.слово pyramis, кот. произошло от егип.слова permeous – «боковое ребро сооружения» или от pyros –«пшеница», или от pyra – «огонь». Заимств. из ст.-сл. яз. Это многогранник, одна из граней которого – плоский многоугольник, а остальные грани – треугольники с общей вершиной, не лежащей в плоскости основания.
Площадь — греч. слово plateia – «широкая». Происхождение неясно. Некоторые ученые считают заимств. из ст.-сл. Другие толкуют как исконно русское.
Планиметрия — лат.слово planum – «плоскость» и metreo – «измеряю». Это часть элементарной геометрии, в которой изучаются свойства фигур, лежащих в плоскости. Т. встречается у древнегреч. ученого Евклида (4 век до н.э.).
Плюс — лат.слово plus – «больше». Это знак для обозначения действия сложения, а также для обозначения положительности чисел. Знак ввел чешский ученый Я. Видман (1489 г.).
Полином — греч.слово polis – «многочисленный», «обширный» и лат.слово nomen – «имя». Это то же, что многочлен, т.е. сумма некоторого числа одночленов.
Потенцирование — немецк.слово potenzieren – «возводить в степень». Действие, заключающееся в нахождении числа по данному логарифму.
Предел — лат.слово limes – «граница». Это одно из основных понятий математики, означающее, что некоторая переменная величина в рассматриваемом процессе ее изменения неограниченно приближается к определенному постоянному значению. Т. ввел Ньютон, а употребляемый ныне символ lim (3 первые буквы от limes) – франц.ученый С.Люилье (1786 г.). Выражение lim первым записал У.Гамильтон (1853 г.).
Призма — греч. слово prisma – «отпиленный кусок». Это многогранник, две грани которого – равные n-угольники, называемые основаниями призмы, а остальные грани – боковые. Т. встречается уже в 3 веке до н.э. у древнегреч. ученых Евклида и Архимеда.
Пример — греч.слово primus – «первый». Задача с числами. Т. изобрели греческие математики.
Производная — франц.слово derivee. Ввел Ж.Лагранж в 1797 году.
Проекция — лат.слово projectio – «бросание вперед». Это способ изображения плоской или пространственной фигуры.
Пропорция — лат.слово proportio – «соотношение». Это равенство между двумя отношениями четырех величин.
Процент — лат.слово pro centum — «со ста». Идея процента возникла в Вавилоне.
Постулат — лат.слово postulatum – «требование». Употребляемое иногда название для аксиом математической теории
Радиан — лат.слово radius – «спица», «луч». Это единица измерения углов. Первое издание, содержащее этот термин, появилось в 1873 году в Англии.
Радикал — лат. слово radix – «корень», radicalis – «коренной». Современный знак ? впервые появился в книге Р.Декарта «Геометрия», изданной в 1637 г. Этот знак состоит из двух частей: модифицированной буквы r и черты, заменявшей ранее скобки. Индийцы называли «мула», арабы – «джизр», европейцы – «радикс».
Радиус — лат слово radius – «спица в колесе». Заимств. в Петровскую эпоху из лат. яз. Это отрезок, соединяющий центр окружности с какой-либо ее точкой, а также длина этого отрезка. В древности Т. не было, он встречается впервые в 1569 г. у франц. ученого П. Раме, затем у Ф.Виета и становится общепринятым в конце 17 века.
Рекуррентный — лат.слово recurrere – «возвращаться назад». Это возвратное движение в математике.
Ромб — греч.слово rombos – «бубен». Это четырехугольник, у которого все стороны равны. Т. употребляется у древнегреческих ученых Герона (1 век до н.э.), Паппа (2-ая половина 3 века).
Рулетты — франц.слово roulette – «колесико», «сравните», «рулетка», «руль». Это кривые. Т. придумали франц. математики, изучавшие свойство кривых.
Сегмент — лат.слово segmentum – «отрезок», «полоса». Это часть круга, ограниченная дугой граничной окружности и хордой, соединяющей концы этой дуги.
Секанс — лат.слово secans – «секущая». Это одна из тригонометрических функций. Обозначается sec.
Секстиллион — франц.слово sextillion. Число, изображаемое с 21 нулем, т.е. число 1021.
Сектор — лат.слово seco – «режу». Это часть круга, ограниченная дугой его граничной окружности и двумя ее радиусами, соединяющими концы дуги с центром круга.
Секунда — лат.слово secunda – «вторая». Это единица измерения плоских углов, равная 1/3600 градуса или 1/60 минуты.
Сигнум — лат.слово signum – «знак». Это функция действительного аргумента.
Симметрия — греч.слово simmetria – «соразмерность». Свойство формы или расположения фигур симметрично.
Синус — лат. sinus –«изгиб», «кривизна», «пазуха». Это одна из тригонометрических функций. В 4-5 вв. называли «ардхаджива» (ардха – половина, джива – тетива лука). Арабскими математиками в 9 в. слово «джайб» — выпуклость. При переводе арабских математических текстов в 12 в. Т. был заменен «синусом». Современное обозначение sin ввел российский ученый Эйлер (1748 г.).
Скаляр — лат.слово scalaris – «ступенчатый». Это величина, каждое значение которой выражается одним числом. Этот Т. ввел ирландский ученый У.Гамильтон (1843 г.).
Спираль — греч.слово speria – «виток». Это плоская кривая, которая обычно обходит вокруг одной (или нескольких) точки, приближаясь или удаляясь от нее.
Стереометрия — греч. слова stereos – «объемный» и metreo – «измеряю». Это часть элементарной геометрии, в которой изучаются пространственные фигуры.
Сумма — лат.слово summa – «итог», «общее количество». Результат сложения. Знак ? (греч. буква «сигма») ввел российский ученый Л.Эйлер (1755 г.).
Сфера — греч. слово sfaira – «шар», «мяч». Это замкнутая поверхность, получаемая вращением полуокружности вокруг прямой, содержащей стягивающий ее диаметр. Т.встречается у древнегреческих ученых Платона, Аристотеля.
Тангенс — лат.слово tanger – «касаться». Одна из тригонометр. функций. Т. введен в 10 веке арабским математиком Абу-л-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Обозначение tg ввел российский ученый Л.Эйлер.
Теорема — греч.слово tereo – «исследую». Это математическое утверждение, истинность которого установлена путем доказательства. Т. употребляется еще Архимедом.
Тетраэдр — греч.слова tetra – «четыре» и edra – «основание». Один из пяти правильных многранников; имеет 4 треугольные грани, 6 ребер и 4 вершины. По-видимому, Т. впервые употреблен древнегреческим ученым Евклидом (3 век до н.э.).
Топология — греч.слово topos – «место». Ветвь геометрии, изучающая свойства геометрических фигур, связанных с их взаимным расположением. Так считали Эйлер, Гаусс, Риман, что Т. Лейбница относится именно к этой ветви геометрии. Во второй половине прошлого столетия в новую область математики, она получила название топологии.
Точка — русс. слово «ткнуть» как бы результат мгновенного прикосновения, укола. Н.И.Лобачевский, впрочем, считал, что Т. происходит от глагола «точить» — как результат прикосновения острия отточенного пера. Одно из основных понятий геометрии.
Трактриса — лат.слово tractus – «вытянутый». Плоская трансцендентная кривая.
Транспозиция — лат.слово transpositio – «перестановка». В комбинаторике перестановка элементов данной совокупности, при которой меняются местами 2 элемента.
Транспортир — лат. слово transortare – «переносить», «перекладывать». Приспособление для построения и измерения углов на чертеже.
Трансцендентный — лат.слово transcendens –«выходящий за пределы», «переходящий». Его впервые употребил немецк.ученый Г.Лейбниц (1686 г).
Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Т. встречается впервые у древнегреческого ученого Посидония (2 век до н.э.).
Триангулированная — лат.слово triangulum – «треугольник».
Тригонометрия — греч.слова trigonon – «треугольник» и metreo –«измеряю». Заимств. в 18 в. из ученой латыни. Раздел геометрии, в котором изучаются тригонометрические функции и их приложения к геометрии. Т. впервые встречается в заглавии книги немецкого ученого Б.Титиска (1595 г.).
Триллион — франц. слово trillion. Заимств. в 18 в. из франц. яз. Число с 12 нулями.
Трисекция — угла лат.слова tri – «три» и section – «разрезание», «рассечение». Задача о разделении угла на три равные части.
Трохоида — греч. слово trochoeides – «колесообразный», «круглый». Плоская трансцендентная кривая.
Тўғри чизиқ — Тўғри чизиқ — геометриянинг асосий тушунчаларидан бири. Тўғри чизиқ геометрияда бошланғич (таърифланмайдиган) тушунча деб олинади. Тўғри чизиқ ва унинг хусусиятлари геометриянинг бошқа тушунчалари билан аксиомалар орқали боғланади. Маcалан, ҳар қандай икки нуқтадан фақат битта тўғри чизиқ ўтади. .
Угол — лат.слово angulus – «угол». Геометрическая фигура, состоящая из двух лучей с общим началом.
Уникурсальный — лат. слова unus – «один», cursus – «путь». Маршрут обхода всех ребер построенного графа, при котором ни одно ребро не проходит дважды.
Факториал (k) — лат.слово factor – «множитель». Впервые появился у французского математика Луи Арбогаста. Обозначение k ввел немецк. математик Кретьен Крамп.
Фигура — лат.слово figura – «внешний вид», «образ». Т. применяемый к разнообразным множествам точек.
Фокус — лат.слово focus – «огонь», «очаг». Расстояние до данной точки. Арабы называли параболу «зажигательным зеркалом», а точку, в которой собираются солнечные лучи – «местом зажигания». Кеплер в «Оптической астрономии» перевел этот Т. словом «фокус».
Формула — лат. слово formula – «форма», «правило». Это комбинация математических знаков, выражающая какое-либо предложение.
Функция — лат. слово functio – «исполнение», «совершение». Одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Т. впервые появляется в 1692 г. у немецк. ученого Г.Лейбница притом не в современном понимании. Т., близкий к современному встречается у швейцарского ученого И.Бернулли (1718 г.). Обозначение функции f(x) ввел российский ученый Л.Эйлер (1734 г.).
Характеристика — греч.слово character – «признак», «особенность». Целая часть десятичного логарифма. Т. был предложен австрийским ученым Г. Бригсом (1624 г.).
Хорда — греч. слово horde – «струна», «тетива». Отрезок, соединяющий две точки окружности.
Центр — лат. слово centrum – «острие ножки циркуля», «колющее орудие». Заимств. в 18 в. из лат. Середина чего-либо, например круга.
Циклоида — греч. слово kykloeides – «кругообразный». Кривая, которую описывает отмеченная точка окружности, катящяяся без скольжения по прямой.
Цилиндр — греч. слово kilindros – «валик», «каток». Заимств. в 18 в. из нем. яз., где zilinder – лат., но восходящее к греч. kylindros. Это тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, перпендикулярными ее оси. Т. встречается у древнегреческих ученых Аристарха, Евклида.
Циркуль — лат. слово circulus – «круг», «обод». Заимств. в первой трети 19 в. из лат. яз. Прибор для вычерчивания дуг, окружностей, линейных измерений.
Циссоида — греч. слово kissoeides – «плющевидный». Алгебраическая кривая. Изобрел греческий математик Диоглес (2 век до н.э.).
Цифры — лат.слова cifra – «цифра», происходящего от арабск.слова «сифр», означающего «нуль».
Числитель — число, показывающее из скольких частей составлена дробь. Т. впервые встречается у византийского ученого Максима Плануда (конец 13 века).
Число ? — (от нач. буквы греч. слова perimetron – «окружность», «преиферия»). Отношение длины окружности к ее диаметру. Впервые появилось у У.Джонса (1706 г.). Стало общепринятым после 1736 года. ? = 3,141592653589793238462…
Шкала — лат.слово scalae – «ступень». Последовательность чисел, служащая для количественной оценки каких-либо величин.
Эвольвента — лат.слово evolvens – «разворачивающий». Развертка кривой.
Экспонента — лат.слово exponentis – «показывающий». То же, что и экспоненциальная функция. Т. ввел немецкий ученый Г.Лейбниц (1679, 1692).
Экстраполирование — лат.слова extra – «сверх» и polio – «приглаживаю», «выправляю». Продолжение функции за пределы ее области определения, при котором продолженная функция принадлежит заданному классу.
Экстремум — лат.слово exstremum – «крайнее». Это общее название максимума и минимума функции.
Эксцентриситет — лат.слова ex – «из», «от» и centrum – «центр». Число, равное отношению расстояния от точки конического сечения до фокуса к расстоянию от этой точки до соответственной директрисы.
Эллипс — греч. слова ellipsis – «недостаток». Это овальная кривая. Т. ввел древнегреческий ученый Апполоний Пергский (260-190 вв. до н.э.).
Энтропия — греч.слово entropia- «поворот», «превращение».
Эпициклоида — греч.слова epi – «над», «на» и kykloeides – «кругообразный». Это плоская кривая, описываемая точкой окружности.
источник
idum.uz